TEOREMA DI PITAGORA E SUE APPLICAZIONI

Enunciazione e spiegazione del teorema

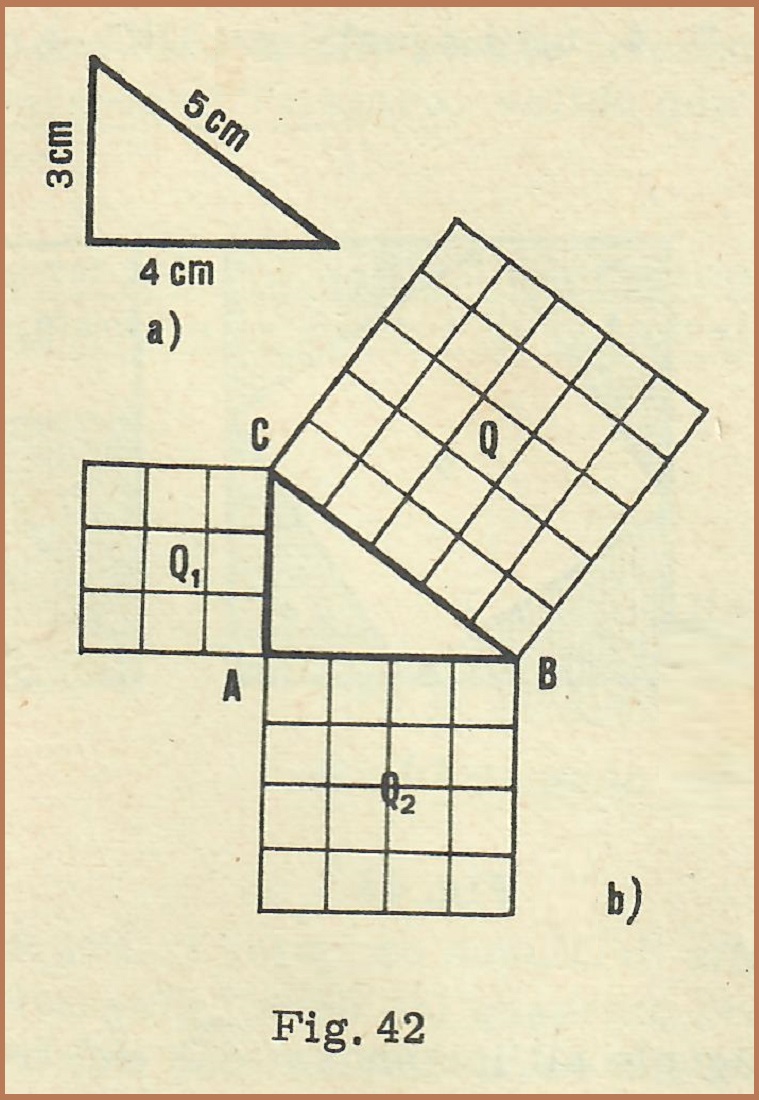
Disegniamo un triangolo rettangolo che abbia i cateti lunghi cm 3 e cm 4 (fig. 42 a) e misuriamo l’ipotenusa: essa è lunga esattamente cm 5.
Costruiamo poi i quadrati Q₁ e Q₂ aventi per lati rispettivamente i due cateti AC ed AB ed il quadrato Q avente per lato l’ipotenusa BC del triangolo. Dividiamo i tre quadrati Q₁ , Q₂ e Q, in quadratini aventi ciascuno il lato lungo cm. 1 (fig. 42 b). Il quadrato Q, costruito sull‘ipotenusa, rimane diviso in 25 quadratini, mentre i quadrati costruiti sui cateti rimangono divisi rispettivamente in 9 e in 16 quadratini uguali ai precedenti.

Osservando che: 9 + 16 = 25 possiamo affermare che, nel triangolo rettangolo considerato, il quadrato Q, costruito sull’ipotenusa, è equivalente alla somma dei quadrati Q₁ e Q₂ , costruiti sui due cateti.

Questa proprietà, come vedremo in seguito, non è una particolarità del triangolo rettangolo che abbiamo considerato, ma può essere estesa a tutti i triangoli rettangoli e prende il nome di teorema di Pitagora. Infatti, si attribuisce a Pitagora, matematico greco vissuto dal 569 al 500 a.C. , l’avere esteso questa proprietà a tutti i triangoli rettangoli. Essa, però, era già nota agli antichi Egiziani, per un triangolo rettangolo con le misure dei lati 3, 4, 5 (ovvero 6, 8, 10; 9, 12, 15).

Verifichiamo ora, sperimentalmente, che il teorema di Pitagora è valido per tutti i triangoli rettangoli, A tale scopo, consideriamo un triangolo rettangolo qualsiasi (figura 43 a); costruiamo poi due quadrati uguali, aventi per lato la somma dei due cateti AB e BC del triangolo dato.

Scomponiamo il primo quadrato (fig. 43 b) nei quattro triangoli 1, 2, 3, 4, tutti uguali ad ABC e nel quadrato Q avente il lato uguale all’ipotenusa AC del triangolo dato.

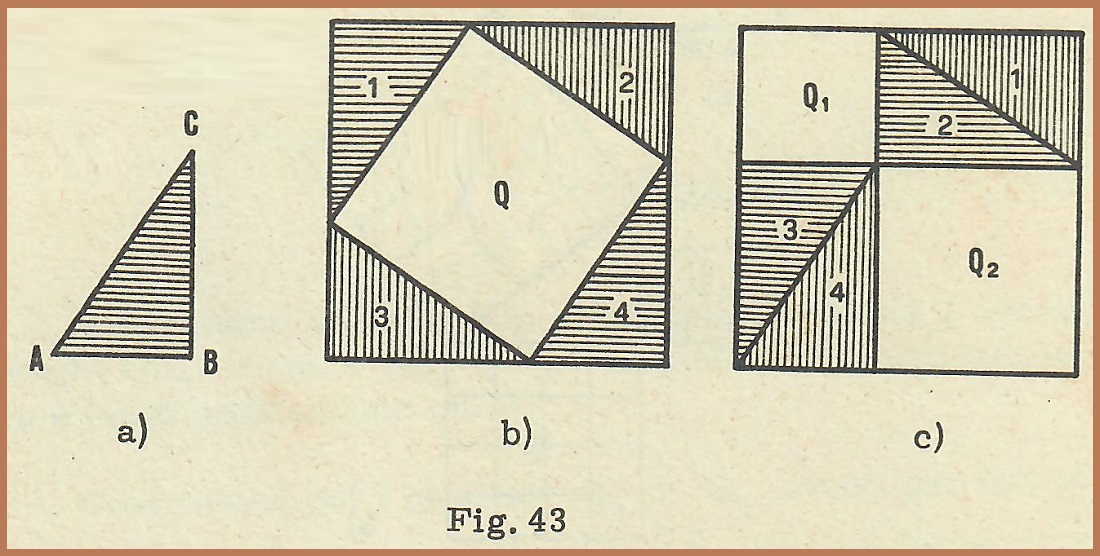
Decomponiamo poi il secondo quadrato (fig. 43 c), nei quadrati Q₁ e Q₂ aventi i lati rispettivamente uguali al cateto AB ed al cateto BC e nei triangoli rettangoli 1, 2, 3, 4, tutti uguali ad ABC.

Se da ciascuno dei due quadrati uguali si tolgono i quattro triangoli rettangoli, rimangono rispettivamente il quadrato Q ed i quadrati Q₁e Q₂ . E ricordando che se da figure uguali sottraiamo figure uguali si ottengono delle figure equivalenti, ne deriva che il quadrato Q è equivalente alla somma dei quadrati Q₁e Q₂.

Poiché Q è il quadrato avente per lato l’ipotenusa del triangolo rettangolo ABC, mentre Q₁e Q₂ sono i quadrati aventi per lati i due cateti dello stesso triangolo, possiamo enunciare il teorema di Pitagora, valido per qualsiasi triangolo rettangolo: in un triangolo rettangolo, il quadrato costruito sull’ipotenusa, è equivalente alla somma dei quadrati costruiti sui cateti.

Relazioni tra le lunghezze dei lati di un triangolo rettangolo

Il teorema di Pitagora ci consente dunque di affermare che in un triangolo rettangolo l’area del quadrato costruito sull’ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui ì cateti. Perciò, se indichiamo con a, b, c, rispettivamente le lunghezze dell’ipotenusa e dei cateti,(fig. 44) di un triangolo rettangolo, tale teorema si può esprimere mediante la formula: a² = b² + c²
da cui si ricava:

Viceversa, poiché c² sommato con b² dà a², ne consegue che c² è uguale alla differenza tra a e b, cioè:
c² = a² – b²
da cui:

analogamente si trova che: b² = a² – c²

In conclusione, queste formule consentono di calcolare la lunghezza di un lato di un triangolo rettangolo quando siano note le lunghezze degli altri due.

Esempio n. 1 – Trovare la lunghezza dell’ipotenusa di un triangolo rettangolo i cui cateti misurano rispettivamente m 9 e m 12.

Esempio n. 2 – Trovare la lunghezza di uno dei cateti di un triangolo rettangolo che ha l’ipotenusa lunga cm 780 e l’altro cateto lungo Km 0,003.

Applicazioni del teorema di Pitagora

Il teorema di Pitagora si applica esclusivamente ai triangoli rettangoli. Se il triangolo non è rettangolo, il quadrato costruito sul lato maggiore, non è mai equivalente alla somma dei quadrati costruiti sugli altri due lati. Esso può però essere applicato nella risoluzione di svariati problemi connessi con tutte le figure geometriche, in quanto tali figure possono essere decomposte in triangoli rettangoli, come appare dagli esempi che seguono.

1) Diagonale di un rettangolo

Disegniamo un rettangolo (fig. 45), con le dimensioni di cm 5 e cm 12 e tracciamo poi la diagonale: osserviamo che essa lo divide in due triangoli rettangoli uguali, ciascuno dei quali ha per cateti due lati consecutivi del rettangolo e per ipotenusa la sua diagonale.

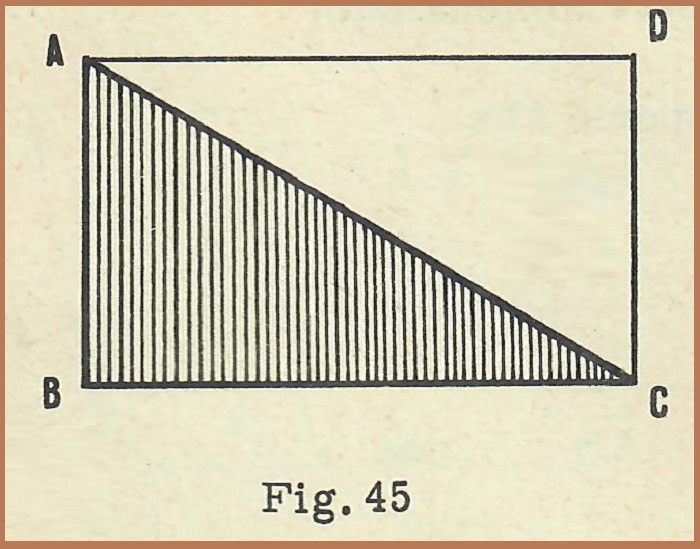
Prendiamo in considerazione uno dei due triangoli rettangoli, ad esempio ABC. Avremo che:

AB = cm 5
BC = cm 12
Per il teorema di Pitagora possiamo dire che:

Quindi: la lunghezza della diagonale di un rettangolo, è uguale alla radice quadrata della somma dei quadrati delle sue dimensioni.
Viceversa se conosciamo la misura di una dimensione del rettangolo e quella della sua diagonale, possiamo trovare quella dell’altra dimensione.
Infatti, supposto che:

2) Diagonale del quadrato

Come possiamo constatare osservando la figura 46, la diagonale di un quadrato lo divide in due triangoli rettangoli isosceli.

Se indichiamo con l la misura del lato del quadrato e con d, quella della sua diagonale, avremo che:

quindi:

Da cui:

Esempio n. 1 – Calcolare la diagonale di un quadrato il cui lato misura cm 3.

Esempio n. 2 – Calcolare la misura del lato del quadrato, sapendo che la sua diagonale misura cm 5,49

3) Altezza di un triangolo isoscele

Vogliamo calcolare la misura dell’altezza di un triangolo isoscele, avente la base di cm 6 ed il lato di cm 8. Sappiamo che l’altezza BH (fig. 47) relativa alla base AC, divide il triangolo nei due triangoli rettangoli uguali AHB e BHC, ciascuno dei quali ha come ipotenusa uno dei lati uguali del triangolo isoscele e, come cateti, l’altezza BH e la metà della base HC (o AH).

Perciò:
AC = cm 6
AB = BC = em8

Quindi:

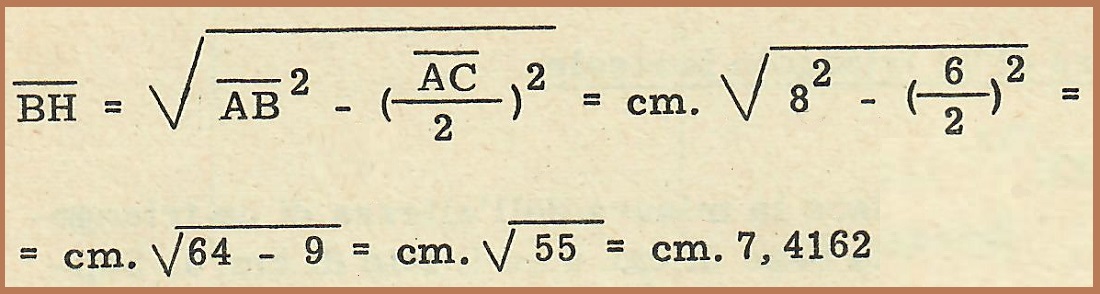
Esempio – L’altezza di un triangolo isoscele misura cm 28 ; ciascuno dei lati uguali misura cm 32. Calcolare l’area del triangolo.

4) Altezza di un triangolo equilatero

Vogliamo calcolare la misura dell’altezza di un triangolo equilatero che ha il lato di lunghezza nota 1. Poiché in un triangolo equilatero tutti i lati sono uguali, indicando con l e con h rispettivamente le lunghezze del lato e dell’altezza (fig. 48), si ha:

e quindi:

Perciò: l’altezza di un triangolo equilatero si ottiene moltiplicando la lunghezza del lato per √3 e dividendo il prodotto per 2.

Esempio n. 1 – Calcolare la misura dell’altezza di un triangolo equilatero, il cui lato misura cm. 10.

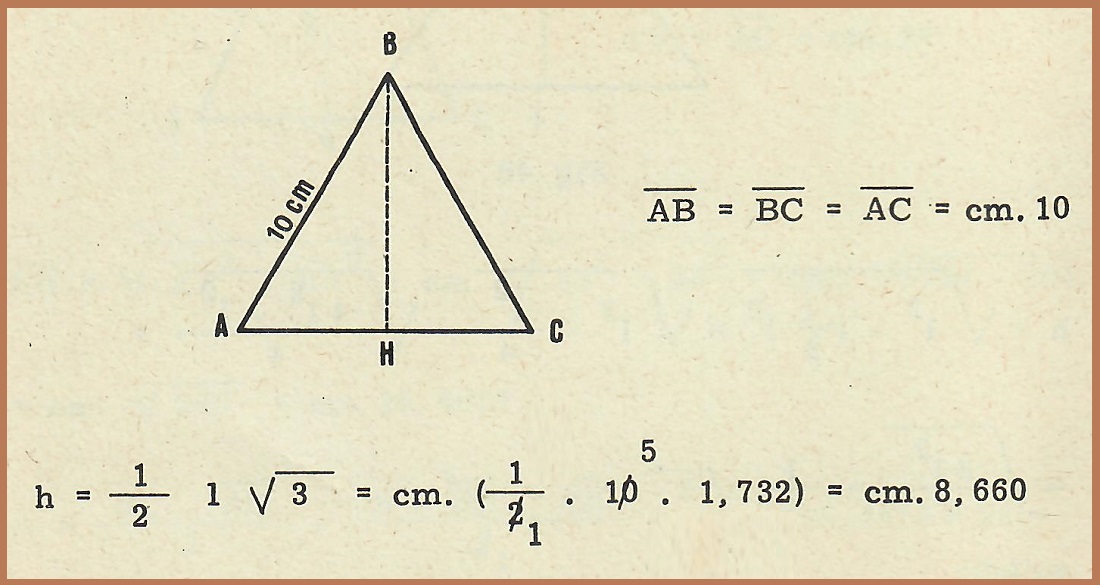
Esempio n. 2 – Calcolare la misura del lato di un triangolo equilatero, che ha l’altezza di cm. 4,33.

5) Applicazione del teorema di Pitagora al rombo

Come possiamo osservare dalla figura 49, le due diagonali dividono il rombo in quattro triangoli rettangoli uguali, ciascuno dei quali ha come ipotenusa il lato del rombo e come cateti le semi diagonali. Perciò, se indichiamo con 1 il lato del rombo e con D e d rispettivamente la diagonale maggiore e la diagonale minore, avremo:

Esempio – Il lato di un rombo misura cm 52 e la diagonale minore è i 10/12 del lato. Calcolare l’area del rombo.

6) Agglicazione del teorema di Pitagora al trapezio rettangolo .

In un trapezio rettangolo possiamo considerare tre triangoli rettangoli, a ciascuno dei quali è possibile applicare il teorema di Pitagora:

– il triangolo rettangolo ADC, che ha per ipotenusa la diagonale maggiore e per cateti l’altezza e la base maggiore (fig. 50 a);

– il triangolo rettangolo BAD, che ha per ipotenusa la diagonale minore e per cateti l’altezza e la base minore (figura 50 b);
– il triangolo rettangolo BHC, che ha per ipotenusa il lato obliquo e per cateti l’altezza ed il segmento HC, differenza delle basi (fig. 500).

Esempio n. 1 – Calcolare l’area di un trapezio rettangolo, sapendo che la base minore misura cm. 7, l’altezza cm. 12 ed il lato obliquo cm. 13.

Esempio n. 2 – Le diagonali e l’altezza di un trapezio rettangolo, misurano rispettivamente dm 273, dm 119, e dm 105. Calcolare l’area e la misura del perimetro del trapezio.

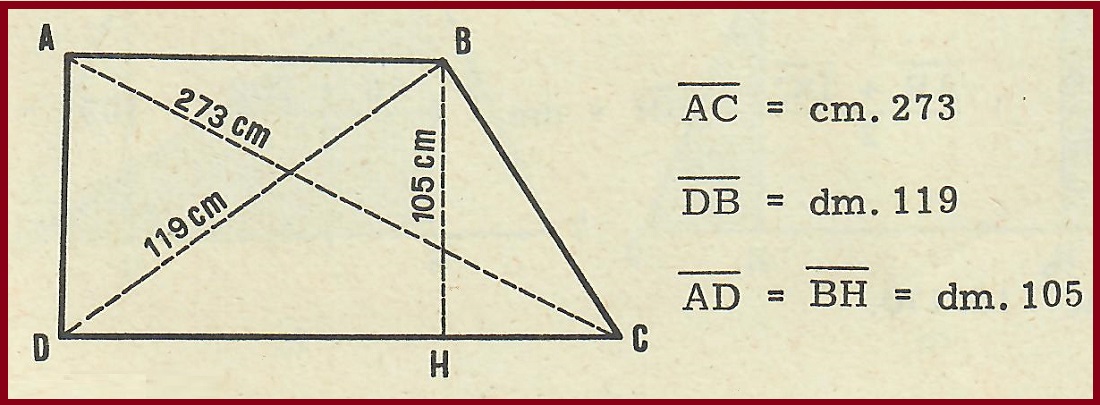
7) Applicazione del teorema di Pitagora al trapezio isoscele

In un trapezio isoscele possiamo considerare due triangoli rettangoli, e precisamente:
– il triangolo rettangolo BHD, che ha per ipotenusa la diagonale e per cateti l’altezza ed il segmento DH uguale ad AB + DH (fig. 51 a);
– il triangolo rettangolo AHD = BH’C, che ha per ipotenusa il lato obliquo e per cateti l’altezza e la semidifferenza delle basi (fig. 51 b).

Esemgio – Un trapezio isoscele ha la base maggiore di
cm. 28, la minore di cm. 18 ed il lato obliquo di cm. 13. Cal—
colare 1’area del trapezio e la lunghezza delle sue diagonali.

8) Applicazione del teorema di Pitagora ai poligoni regolari

Anche un poligono regolare può essere scomposto in tanti triangoli rettangoli uguali (fig. 52), in cui l’ipotenusa è data dal raggio del poligono regolare e i cateti sono rispettivamente l’apotema e metà lato del poligono stesso.

9) Applicazione del teorema di Pitagora ai poligoni inscritti e circoscritti ad una circonferenza.

a – Se conosciamo le lunghezze delle diagonali di un rombo, il teorema di Pitagora ci permette di calcolare la lunghezza del raggio della circonferenza a cui il rombo è circoscritto (fig. 53). Tale raggio non è altro che l’altezza relativa all’ipotenusa di ciascuno dei quattro triangoli rettangoli in cui il rombo viene diviso dalle diagonali.

Esempio – Determinare il perimetro di un rombo ed il raggio del cerchio in esso inscritto, sapendo che l’area è m 2 47,04 e che una sua diagonale è lunga m 8,4.

b – Come già sappiamo, l’apotema di un poligono regolare, si ottiene moltiplicando la misura del lato per un opportuno numero, variabile a seconda del numero dei lati del poligono. Vogliamo ora renderci ragione di questo numero nel caso dell’esagono regolare.

Nella figura 54, O è il centro dell’esagono regolare ABCDEF ed il triangolo OAB, come sappiamo, è un triangolo equilatero il cui lato è il lato dell’esagono regolare e la cui altezza OH è l’apotema. Se ora consideriamo il triangolo rettangolo CHA, avremo che:

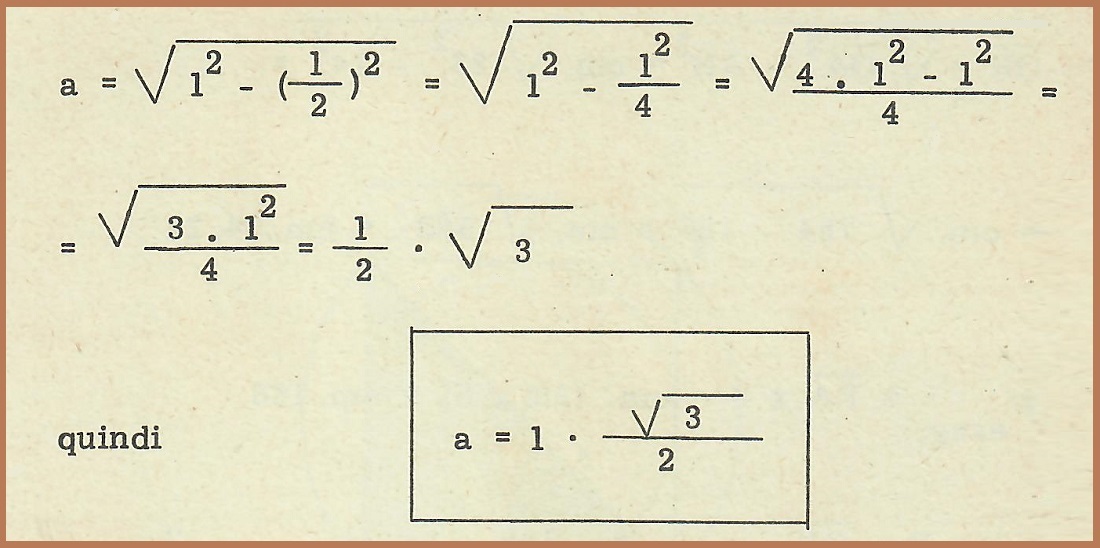
Il numero 0,866 è il valore approssimato a meno di un millesimo per difetto di √3/2 , ed è appunto il numero fisso di cui si è già parlato nel caso dell’esagono regolare.

Esempio – Calcolare l’area di un esagono il. cui lato misura cm. 28

10) Applicazione del teorema di Pitagora a un quadrato inscritto e circoscritto

Se osserviamo la figura 55, noteremo che la diagonale AC del quadrato inscritto non è altro che il diametro della circonferenza ad esso circoscritta. Poiché già sappiamo che la misura della diagonale di un quadrato si può calcolare applicando il teorema di Pitagora basterà conoscere la misura del lato per calcolare la misura del diametro della circonferenza circoscritta e quindi anche la misura del raggio del quadrato.

Sempre dalla figura 55 è facile verificare che la circonferenza inscritta in un quadrato, ha per diametro il lato di quest’ultimo. Perciò l’apotema del quadrato, che è anche il raggio della circonferenza inscritta, è uguale metà lato.

Esempio – Un quadrato ha l’area di cm² 1.024. Calcolare il raggio della circonferenza inscritta e quello della circonferenza circoscritta al quadrato.

11) Applicazione del teorema di Pitagora al cerchio

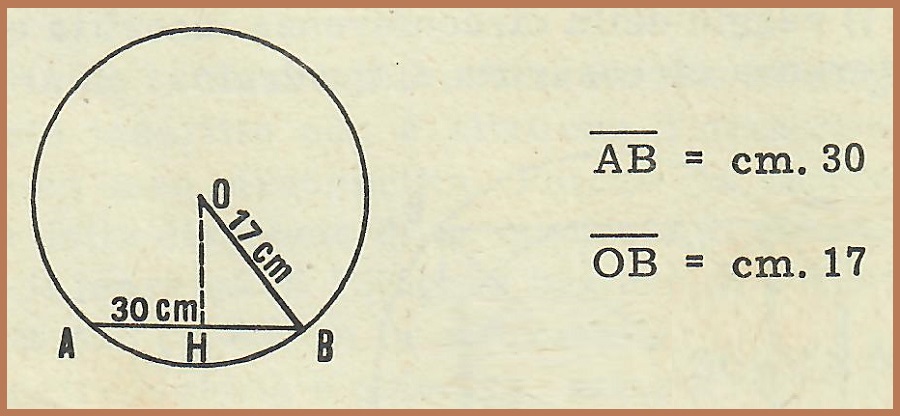
In una circonferenza il raggio misura cm 17 ed una sua corda AB misura cm 30. Determinare la distanza OH della corda dal centro.

Figure con angoli particolari

Sono considerate figure particolari, quelle che presentano un angolo di 30° o di 45° 0 di 60° ; per esse si possono ricavare alcune relazioni fra i lati, che ci permettono di risolvere numerosi problemi.

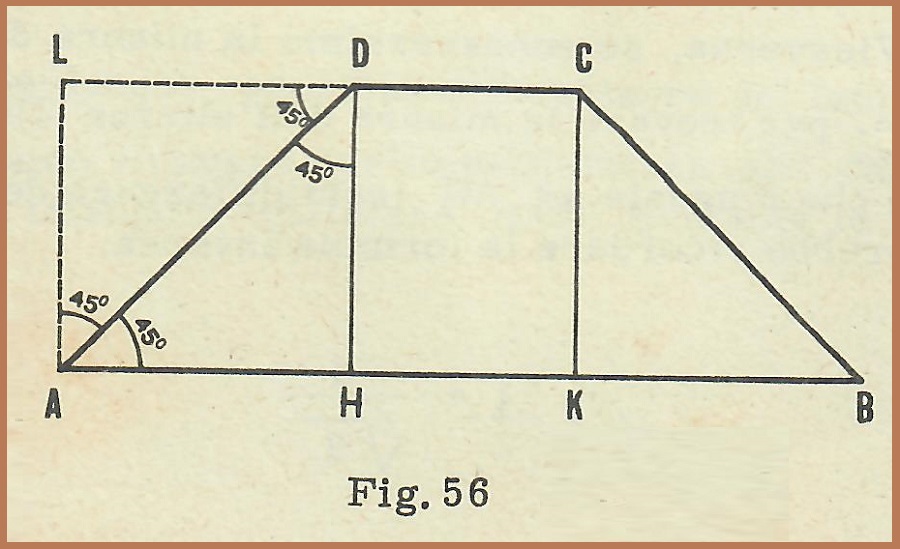
1) Consideriamo il trapezio isoscele ABCD (fig. 56), in cui il lato obliquo AD forma un angolo di 45° con la base maggiore AB. Prolunghiamo la base minore e tracciamo poi la perpendicolare alla base maggiore passante per il vertice A: sia L il punto d’intersezione tra la perpendicolare e il prolungamento della base minore. La figura che abbiamo ottenuto, AHDL, è un quadrato, che ha come diagonale il lato obliquo AD del trapezio. Ovviamente l’altezza DH del trapezio, lato del quadrato DHAL, è uguale al segmento AH (cioè alla semidifferenza delle basi).

Perciò, se conoscessimo l’altezza DH del trapezio, potremmo ricavare la misura del lato obliquo sia applicando il teorema di Pitagora al triangolo rettangolo isoscele DHA, sia ricordando la formula:che ci permette di ricavare la misura della diagonale di un quadrato conoscendo la lunghezza di un lato.

Viceversa, se conoscessimo la misura del lato obliquo, per trovare la misura dell’altezza DH del trapezio che è uguale ad AH (semidifferenza delle basi), basterebbe ricordare la formula inversa:

2) Consideriamo ora il trapezio isoscele ABCD in cui il lato obliquo AD forma un angolo di 60° con la base maggiore AB (fig. 57). Tracciamo l’altezza DH e disegniamo un triangolo DHL uguale a DHA, Il triangolo DAL, così ottenuto, è, ovviamente, un triangolo equilatero. Perciò il lato obliquo DA è uguale ad AL e quindi il doppio della semidifferenza delle basi.

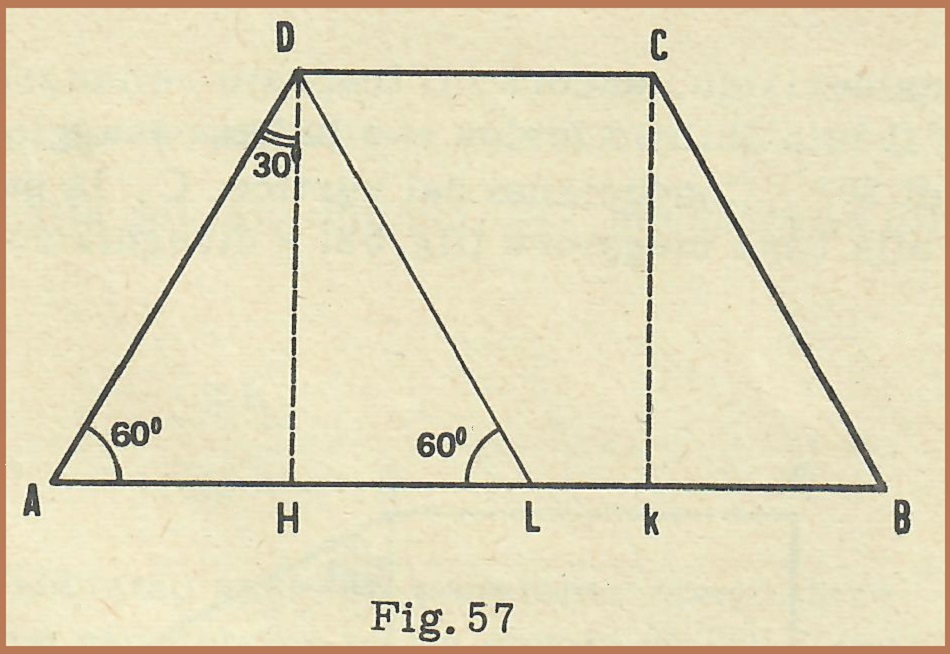
Se dunque conosciamo la misura del lato obliquo, possiamo ricavare quella dell’altezza DH del trapezio (e del triangolo equilatero DAL) mediante la formula nota:

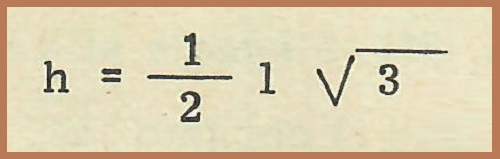
Viceversa, conoscendo la misura dell’altezza DH, potremmo ricavare quella del lato obliquo DA mediante la formula inversa:

3) Consideriamo, ancora, il trapezio rettangolo ABCD in cui il lato obliquo forma con la base maggiore un angolo di 30°. Conduciamo dal vertice C, la perpendicolare alla base maggiore (fig. 58) e disegniamo ora il triangolo rettangolo BHL, uguale a BHC. Il triangolo BCL così ottenuto è ovviamente un triangolo equilatero, la cui altezza BH è uguale alla semidifferenza delle basi del trapezio ed il cui lato BC è il doppio dell’altezza CH del trapezio.

Perciò se noi conosciamo la misura del lato obliquo del trapezio, possiamo ricavare la misura BH della differenza delle basi mediante la nota formula:

Viceversa, se conosciamo la misura di BH, possiamo ricavare quella del lato obliquo BC mediante la formula inversa:

Da quanto abbiamo appreso possiamo concludere che se una figura geometrica ha un angolo di 45°, noi possiamo costruire un quadrato e sfruttare le relazioni esistenti fra il lato e la diagonale.

Se in una figura geometrica vi è un angolo di 30° 0 di 60°, possiamo costruire un triangolo equilatero e sfruttare le relazioni esistenti tra il lato e l’altezza.

Esempio n. 1 – Un trapezio rettangolo ha l’angolo acuto di 45°, l’altezza di cm 8 e la base minore di cm 6. Calcolare l’area e la misura del perimetro del trapezio.

Esempio n. 2 – In un triangolo rettangolo, che ha un angolo acuto di 60°, il cateto minore misura cm 15. Calcolare il perimetro.

Da questo esempio si può dedurre che se un triangolo rettangolo ha un angolo di 60° (e quindi l’altro di 30°); il cateto opposto all’angolo di 30° è la metà dell’ipotenusa.