ENTI GEOMETRICI FONDAMENTALI - Punto, linea, retta, segmento

ENTI GEOMETRICI FONDAMENTALI

Scopo della geometria

Secondo Erodoto, storico greco (500 – 424 a. C.), la geometria sarebbe nata in Egitto a causa della necessità di ripristinare i confini di proprietà cancellati ogni anno dalle piene del Nilo; infatti la parola significa, letteralmente,
“misura del terreno”. Scopo della geometria è lo studio delle proprietà che si riferiscono alla forma e all’estensione dei corpi (cioè degli innumerevoli oggetti che ci circondano), prescindendo dalle sostanze di cui essi sono costituiti (ferro, acciaio, legno, vetro, ecc.).

È bene tener presente che forma ed estensione dei corpi, sono due proprietà distinte: infatti un pallone per il giuoco del calcio ed una pallina da ping-pong hanno la stessa forma (forma sferica), ma non la stessa estensione (infatti i due corpi non occupano la stessa porzione di spazio).

Un barattolo ed un mattone hanno forma diversa, ma possono occupare la stessa porzione di spazio e quindi avere la stessa estensione.

Un corpo del quale si prendono in esame unicamente la forma e l’estensione, trascurandone tutte le altre proprietà (colore, peso, materia di cui il corpo ’è costituito, ecc. ), si dice solido geometrico.

*** * * * ***

Superficie

Ogni solido geometrico è separato dallo spazio che lo circonda da una superficie; tale superficie costituisce quindi l’elemento di separazione di ogni corpo dal resto dello spazio circostante. L’idea di superficie ci può essere fornita dalla pellicola che delimita una bolla di sapone, dal guscio di un uovo, dalla buccia di un frutto, ecc. Ogni superficie può essere piana (ad esempio quella della faccia di un mattone) o curava (ad esempio quella di un pallone o di un uovo) e deve essere immaginata priva di spessore e non costituita da materia. Fra le tante superfici che possono essere immaginate, hanno particolare importanza le superfici piane.

*** * * * ***

Piano

L‘idea di una superficie piana, ci può essere data da un foglio di carta ben teso su un tavolo, dal piano stesso di un tavolo, dalla superficie di uno stagno d’acqua in quiete, ecc.
Tali superfici hanno però una estensione limitata: la superficie geometrica-piana, detta anche giano, invece, è indefinitamente estesa in tutte le direzioni, come una gran pianura che si estenda da ogni parte a perdita d‘occhio.
Perciò si dice che il giano è illimitato.
I piani, in geometria, si indicano con le lettere dell’alfabeto greco α (alfa), β (beta), γ (gamma), ecc.

*** * * * ***

Punto

Se poggiamo la punta aguzza di una matita su un foglio di carta, o se buchiamo questo foglio con la punta di un ago, la traccia lasciata dalla matita o dall’ ago, ci dà l’idea intuitiva del punto. Il punto geometrico, però, deve essere immaginato privo di estensione e di materia, cioè senza dimensioni.
Un punto si indica con una lettera maiuscola dell’alfabeto (fig. 1).

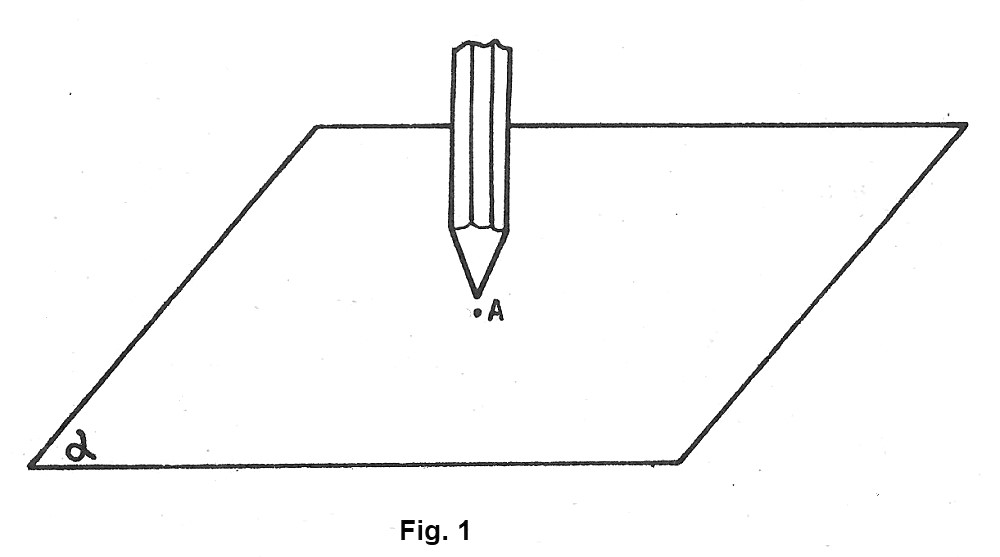
Un insieme di innumerevoli punti, si dice figura geometrica. Tale figura si dice piana, se tutti i suoi punti sono situati su uno stesso piano; si dice solida, se i suoi punti sono situati in piani diversi. Ad esempio, l’immagine che compare sullo schermo di un televisore è formata da innumerevoli punti, talmente fitti, che noi non riusciamo a distinguerli singolarmente; essi, tutti insieme, danno al nostro occhio, l’impressione di una figura. Perciò possiamo dire che la figura è un insieme di punti.

*** * * * ***

Linea

La traccia lasciata dalla punta della matita che scorre su un foglio di carta, su un rotolo o su una palla, ci dà l’idea intuitiva di una linea (fig. 2 a, b, c).

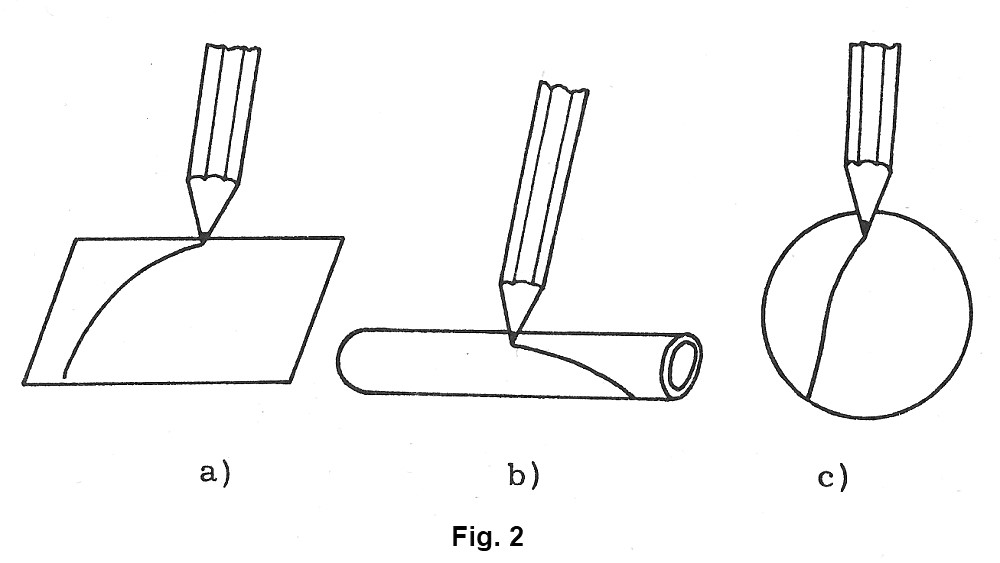
La linea geometrica si deve immaginare senza alcuno spessore.

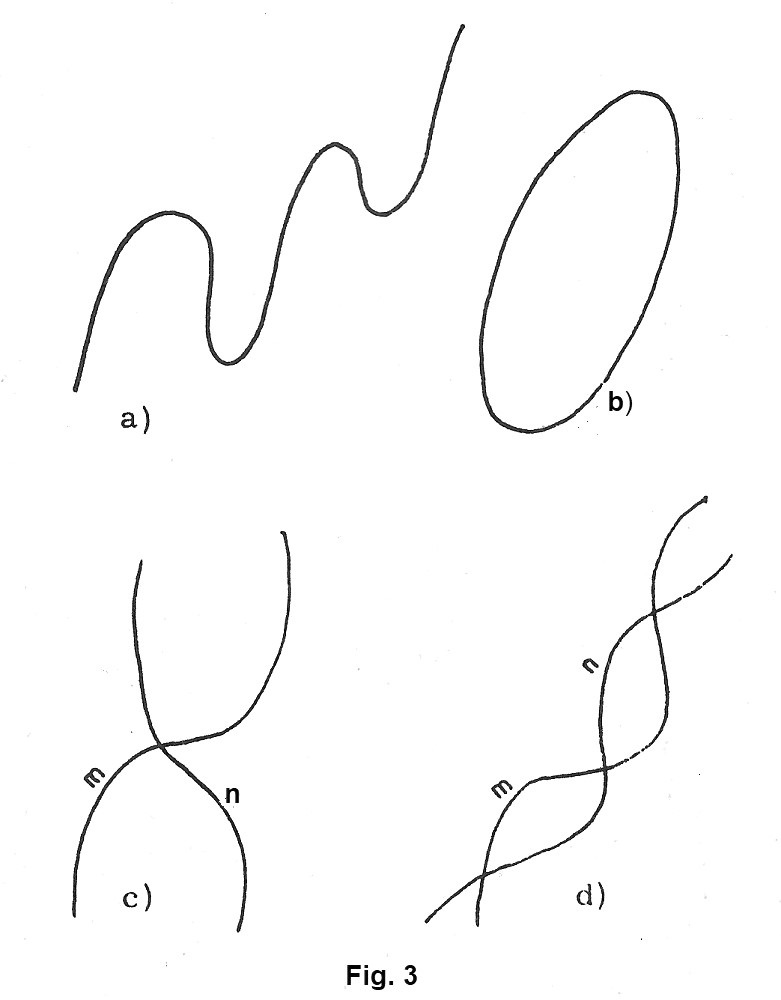
Una linea può essere aperta (fig. 3 a) o chiusa (fig. 3 b), a seconda che i suoi estremi siano congiunti o disgiunti. Per distinguere una linea dall’altra, basterà indicare ciascuna di esse con una lettera minuscola dell’alfabeto.

Due linee si possono intersecare in un punto (fig. 3 c) o in più punti (fig. 3 d). I punti comuni a due linee m e n si dicono punti di intersezione delle due linee.

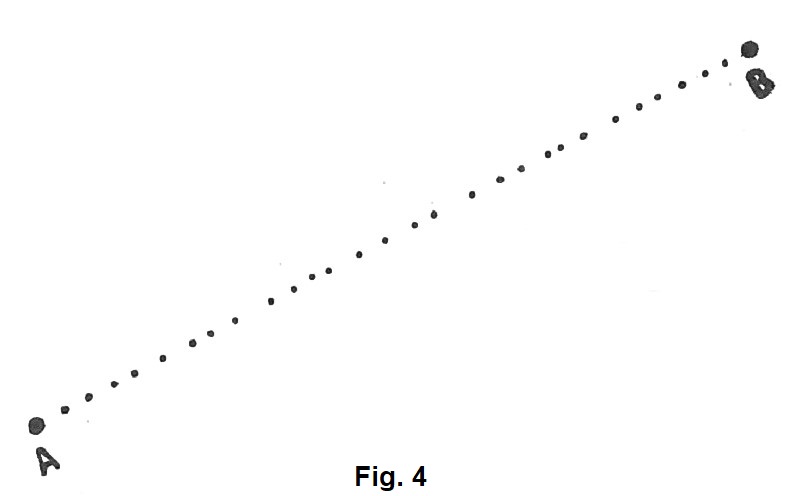
Se tracciamo su un piano un punto A ed un punto B, distanti l’uno dall’altro e disegniamo poi un insieme di punti allineati, che vanno dal punto A al punto B (fig. 4), otteniamo una linea. Possiamo quindi “dire che: ogni linea è un insieme di innumerevoli punti. Tali punti,
infatti, non si possono contare perché, fra due di essi, per quanto vicini, ve ne sono sempre degli altri.

*** * * * ***

Linea retta

Se poggiamo un filo su un tavolo, questo filo acquisterà una forma curva; ma se ne tendiamo gli estremi, esso di- venterà diritto e si potrà appoggiare, ad esempio, sul bordo di una riga. Un filo ben teso, ci dà l’immagine di una linea retta o retta (fig. 5).

Per rappresentare una retta, su un foglio di carta, basterà far scorrere una matita lungo il bordo di una riga poggiata su di esso. La retta che noi possiamo disegnare può essere più o meno lunga, ma comunque sempre limitata.

La retta geometrica deve invece essere concepita come illimitata in entrambi i sensi (cioè senza inizio, né fine).

Possiamo perciò dire che: una retta è illimitata.

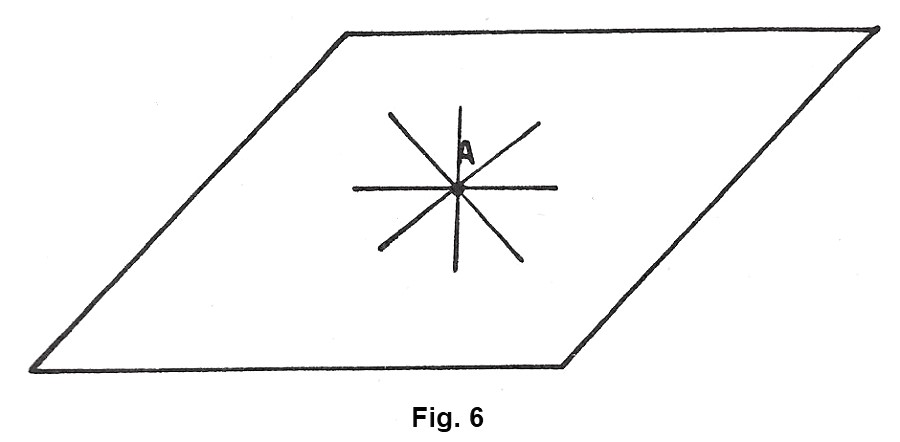
Fissiamo ora, su un piano, un punto A (figura 6) e disegniamo alcune rette che passano per A. Ci rendiamo facilmente conto che è possibile far passare, per tale punto, quante rette vogliamo.
Perciò possiamo dire che: per un punto passano infinite rette.

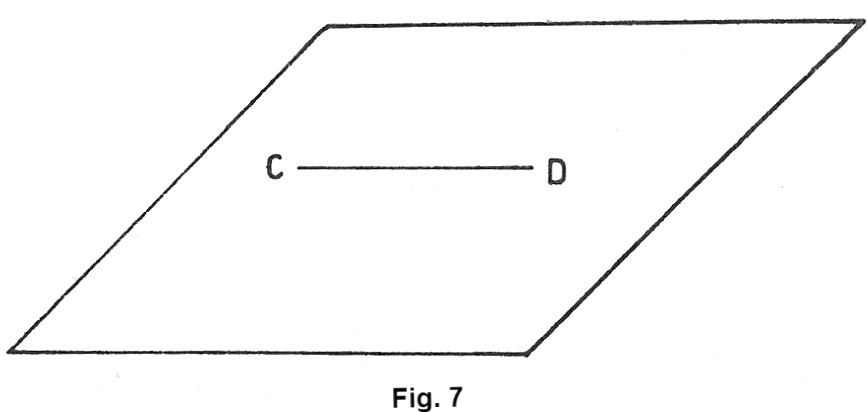
Disegniamo ancora due punti C e D (figura 7) e proviamo a tracciare qualche retta passante sia per C che per D. Vedremo che non è possibile tracciar-ne più di una.
Perciò possiamo dire che: per due punti passa una sola retta.

*** * * * ***

Semiretta

Disegniamo una retta r (figura 8) e fissiamo su di essa un punto O; il punto divide la retta in due partì, ciascuna delle quali è detta semiretta. Il punto O si dice origine di ciascuna delle due semirette.

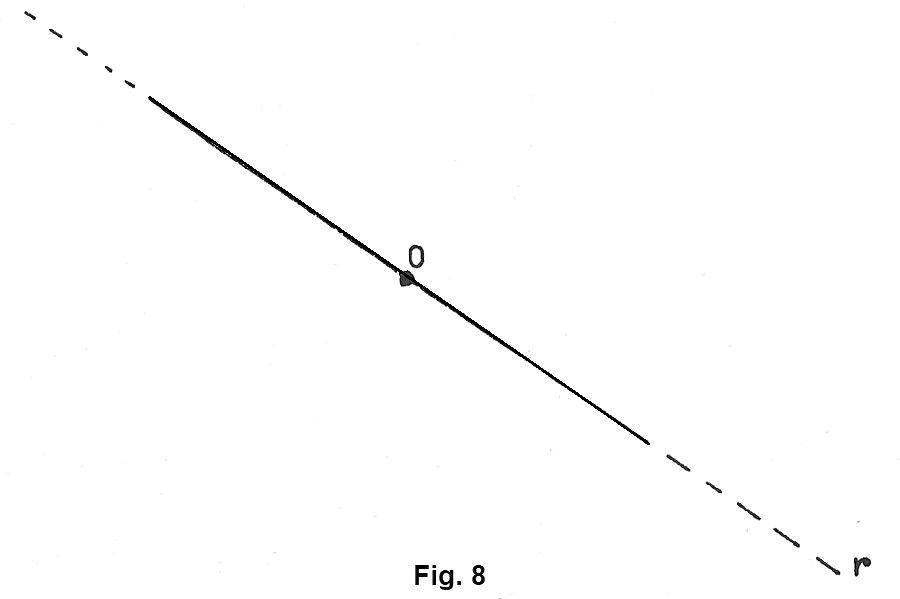
È evidente che una semiretta è illimitata in una sola direzione.

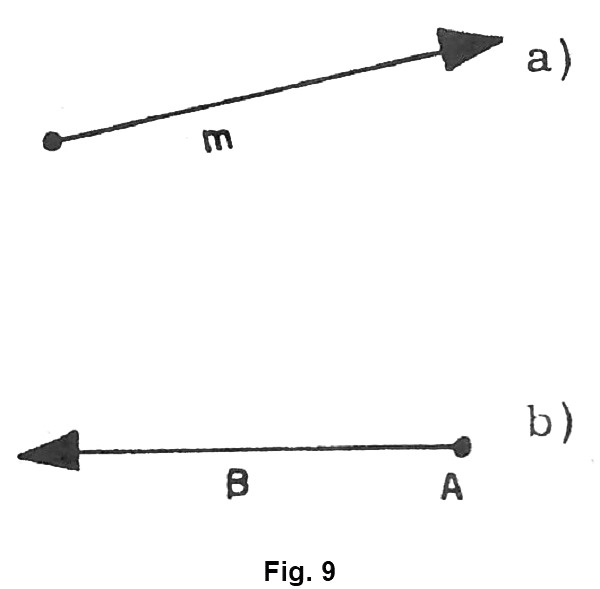
Le semirette vengono indicate con una lettera minuscola dell’alfabeto (fig. 9 a), Oppure denominandone l’origine ed un altro punto qualunque, ad esempio: semiretta AB (figura 9 b). Quindi possiamo dire che: la semiretta è ciascuna delle due parti che si ottengono fissando su di una retta un punto.

*** * * * ***

Segmento

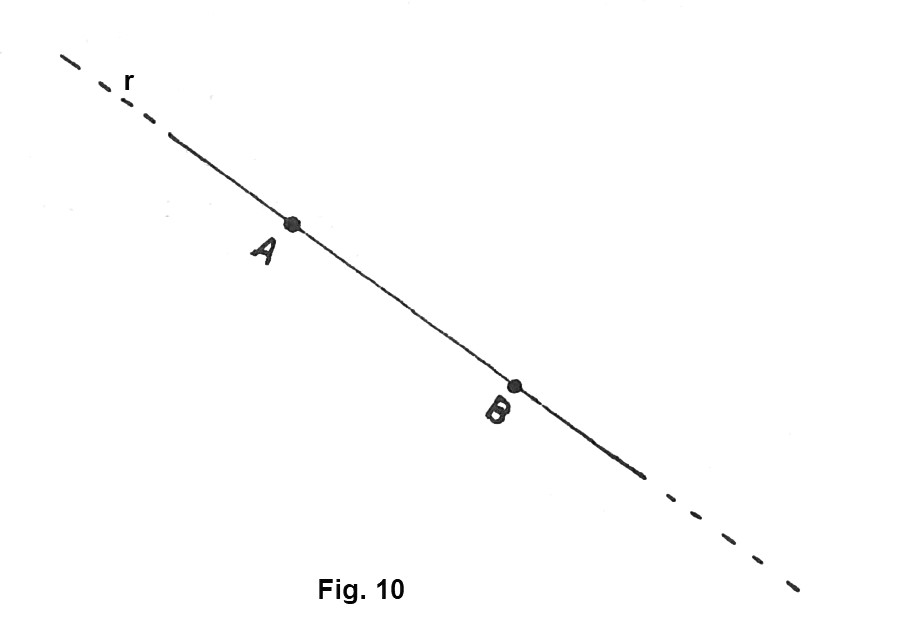
Disegniamo una retta r e fissiamo su di essa due punti A e B (fig. 10). La retta risulta così divisa in tre parti: una parte è compresa tra i due punti A e B, le altre due parti si trovano rispettivamente a sinistra di A e a destra di B e sono, ovviamente, due semirette.

La parte di retta, compresa tra i punti A e B, si dice segmento e i due punti si dicono estremi del segmento.

Le due semirette di origine A e B, si dicono anche prolungamenti del segmento.

Per indicare un segmento si scrivono le lettere dei suoi estremi una accanto all’altra. Così il segmento avente per estremi il punto A ed il punto B si indica con AB (AB con un righino sopra, che sta ad indicare appunto che si tratta di un segmento).

È evidente che il segmento è limitato in ambedue i sensi. Perciò possiamo dire che: il semento è una parte di retta compresa tra due punti che si dicono estremi del segmento.
Il segmento rappresenta anche la distanza fra i due punti, cioè il percorso più breve tra i due punti stessi.

*** * * * ***

Segmenti consecutivi e segmenti adiacenti

Se, ad esempio, disponiamo due strisce di carta (figura 11), ciascuna con un foro ad una estremità, in modo da sovrapporre i due fori e le fissiamo con un ferma-campioni, possiamo dire di aver disposto consecutivamente le due strisce. Esse ci forniscono un’immagine concreta di due segmenti consecutivi, come sono i segmenti AB e BC della figura 12. Quindi possiamo dire che: due segmenti si dicono consecutivi, quando hanno un estremo in comune.
Ovviamente si possono anche avere più segmenti consecutivi (fig. 13).

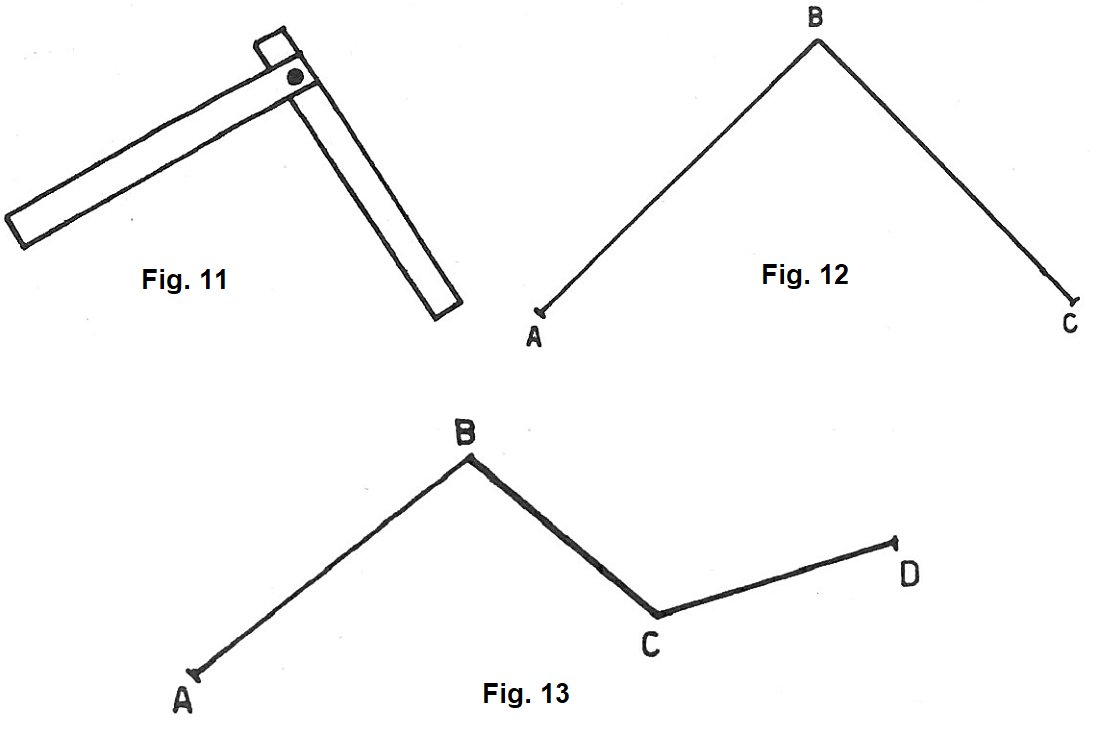
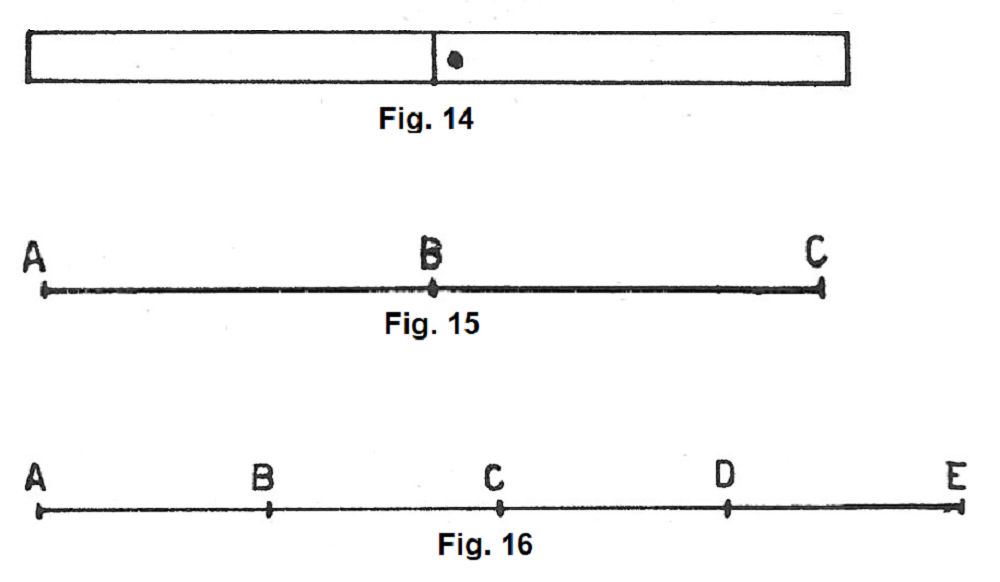
Se teniamo ferma una delle strisce di cui alla figura 11 e facciamo ruotare l’altra intorno al fermacampioni, finché viene ad essere allineata con la prima, le due strisce risultano disposte sulla stessa retta (fig. 14). Diciamo allora che le due strisce sono una adiacente all’altra,

Esse ci forniscono l’immagine concreta di due segmenti adiacenti, come lo sono i segmenti AB e BC della figura 15.

Quindi possiamo dire che: due segmenti si dicono adiacenti quando sono consecutivi ed appartengono alla stessa retta.

Ovviamente si possono avere più di due segmenti consecutivi (fig. 16).