MECCANICA APPLICATA
IL BARICENTRO
“Si definisce baricentro di un sistema di masse (o forze), il punto intorno al quale ruota la risultante del sistema”.
Dalla definizione si deduce che il baricentro di un sistema di masse (o forze) è quel punto ove possiamo pensare concentrata tutta la massa del sistema e che risulta indipendente dalla comune direzione che si assegna ai vettori rappresentativi delle masse (o forze), concentrate nei punti. In altri termini il baricentro di un sistema resta fisso quando i vettori rappresentativi delle masse ruotano concordemente mantenendosi fra loro paralleli.
Determinazione grafica del baricentro
Dalla definizione del baricentro discende il modo abbastanza semplice per la sua determinazione grafica. Basta considerare, infatti, le masse del sistema dato m1 , m2 …. mi come moduli di vettori tutti paralleli tra loro applicati rispettivamente in A1 , A2, …. Ai.
Costruita la punteggiata l, 2, ….i delle grandezze, connettere il detto sistema di vettori con un poligono funicolare di polo P.
Determinare il punto di incontro del primo ed ultimo latto del poligono funicolare e tracciare per questo la retta di azione della risultante, dopo, ripetere la stessa costruzione ruotando concordemente il sistema di vettori fra loro paralleli di un angolo a piacere. .
La nuova direzione della risultante incontrerà la prima direzione nel punto G che è il baricentro cercato.
Un esempio chiarirà detta costruzione (vedi figura 23).

Consideriamo le quattro masse m1, m2, m3 ed m4 e pensate queste come moduli di vettori F1, F2, F3 ed F4 tutti paralleli tra loro applicati rispettivamente in A1, A2, A3, A4 si è costruita la punteggiata O, 1, 2, 3, 4 (i valori delle masse sono riportati della figura 23),
Scelto il polo P si sono proiettati i punti O, 1, 2, 3, 4, della punteggiata e si è, com’è noto, costruito il poligono funicolare O1,, 11, 21, 31, 41, 51; si è prolungato il primo lato O111 e l’ultimo lato 5141del poligono funicolare fino all’incontro nel punto B, per il quale tracceremo la direzione R della risultante.
Facendo ruotare concordemente il sistema di vettori fra loro paralleli di un angolo di 90° si ridisegna la punteggiata nella nuova posizione ruotata di 90° rispetto alla precedente e si ruotano dello stesso angolo di 90° le rette di azione del sistema di vettori.
Si traccia il nuovo poligono funicolare e, quindi, la nuova retta di azione R1 della risultante che passerà per il punto C.
L’incontro delle rette R ed R1 nel punto G individueranno il baricentro cercato.
Si può evitare di disegnare la seconda punteggiata delle masse (o forze) e i relativi vettori ruotati di 90°, in quanto i lati dei due poligoni funicolari, corrispondenti al medesimo vettore, sono perpendicolari tra loro come si può facilmente vedere dalla figura 23. Basterà, quindi, tracciato il primo poligono funicolare, per i punti A1, A2, A3, A4 condurre le perpendicolari ai lati del poligono disegnato, ottenendo così direttamente il secondo poligono funicolare ruotato di 90° rispetto al primo.
Proprietà del baricentro
a – Il baricentro di un sistema di masse resta invariato se tutte le masse si moltiplicano per uno stesso numero.
b – Se le masse m1 hanno tutte lo stesso segno, il baricentro G è interno ad ogni linea chiusa convessa che racchiude tutti i punti A1; in particolare se i punti A1 di applicazione delle masse appartengono ad una retta, il baricentro è interno al segmento individuato dai punti estremi.
c – Se il sistema dato lo si considera decomposto in due sistemi parziali, cui corrispondono i baricentri parziali G1 e G2, il baricentro totale G coincide col.
baricentro dei due sistemi G1 e G2, sedi rispettivamente delle masse parziali (proprietà distributiva).
Assi diametrali e di simmetria
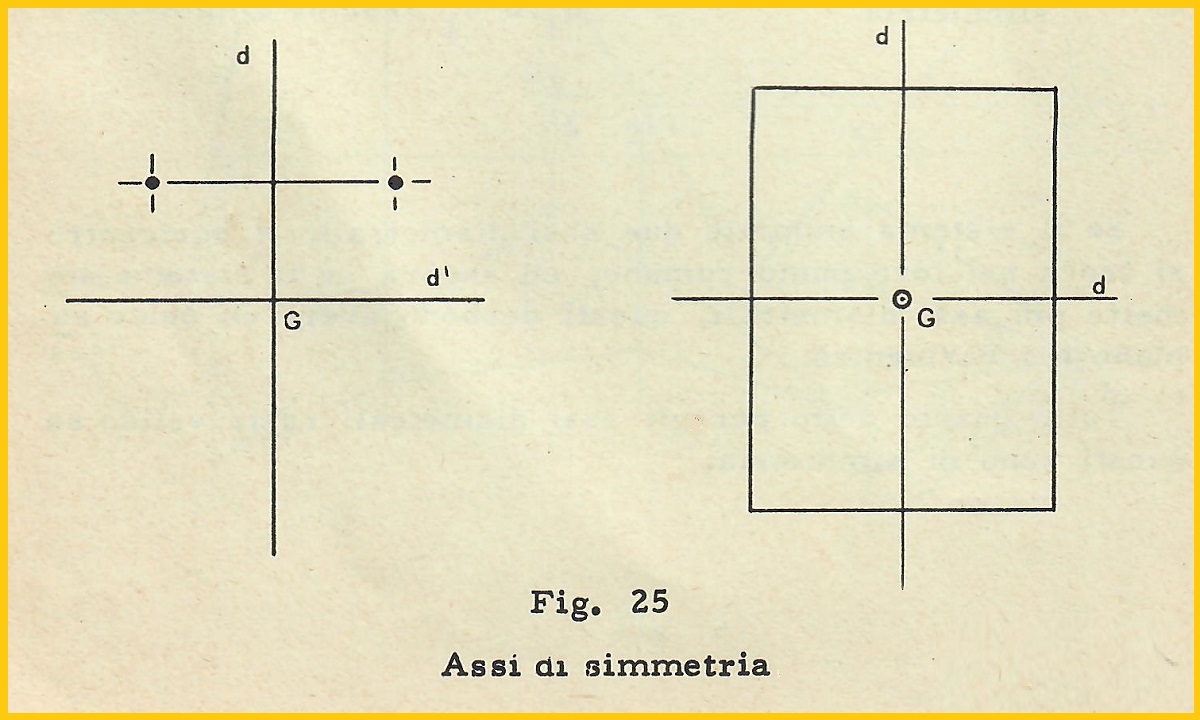
Diremo che un dato sistema possiede un asse diametrale d, coniugato ad un’assegnata direzione d1, quando ad ogni punto A1 del sistema, sede di una massa m1, fa riscontro un punto situato sulla parallela a d1 per A1 alla stessa distanza da d, ma da banda opposta, sede di un’eguale massa m1: tali punti li diremo coniugati (vedi figure 24 e 25).

Assi diametrali
“Quando d è perpendicolare a d1, d è detto ASSE di SIMMETRIA” (vedi figura 25).
Osserviamo che il baricentro di un sistema di vettori paralleli e concordi costituito da due soli vettori eguali, coincide con il punto medio del segmento congiungente i due punti di applicazione, segue che, se il sistema ammette un asse diametrale, noi potremo (per la proprietà distributiva) pensarlo costituito da tante parti quante sono le coppie di punti coniugati; i baricentri delle singole coppie giacciono sull’asse diametrale e, quindi, il baricentro totale giace sullo stesso asse diametrale (vedi figura 26).

Se il sistema ammette due assi diametrali, il baricentro si trova nel loro punto comune, ed ancora se il sistema ammette più assi diametrali, questi debbono avere un punto comune nel baricentro.
Tutto quanto detto per gli assi diametrali resta valido se questi sono di simmetria.
Baricentri di alcune linee
Baricentro di una spezzata irregolare ABCDE (vedi figura 27) – Applicando la proprietà distributiva, penseremo suddiviso il sistema in tanti segmenti quanti sono i lati della spezzata.
Il baricentro di uno di tali lati, per esempio AB, è, come sappiamo, un punto di AB interno ad AB e, poiché questo ammette un asse di simmetria nella normale condotta per il suo punto di mezzo, il baricentro di A B sarà il suo punto di mezzo G1 così dicasi per gli altri lati della spezzata: il problema è, in tal modo, ricondotto alla determinazione del baricentro dei punti G1, G2, G3, G4, sedi rispettivamente di masse proporzionali alle lunghezze dei singoli lati della spezzata.

Applicando, quindi, la costruzione già trattata, si determina il baricentro G.
Baricentro di un arco circolare (vedi figura 28) – La perpendicolare alla corda AB per il centro C è asse di simmetria dell’arco, quindi il baricentro G si troverà su di esso.
La distanza yG dal centro C del baricentro dell’arco di circonferenza, si può determinare con la seguente costruzione grafica:

si riportata lungo la tangente all’arco in H una lunghezza HL uguale all’arco HB rettificato (*).
Si congiunge il punto L con C e dall’estremo B dell’arco di circonferenza si tracci la parallela all’asse HC fino ad incontrare nel punto T il segmento CL.
Dal punto T si conduce la parallela alla HL fino ad incontrare in G l’asse di simmetria.
Il punto G è il baricentro cercato.
(*) Rettificare un arco significa determinare la sua lunghezza l e disegnarla lungo una retta; tale lunghezza è data dalla formula seguente:

in cui π = 3,14; r è il raggio dell’arco di circonferenza; φ è l’angolo che l’asse di simmetria forma con la congiungente l’estremo dell’arco con il centro C.
VEDI ANCHE . . .
.
