GEOMETRIA - GLI ANGOLI - Blog di pociopocio

ANGOLI

Poggiamo su un foglio di carta due strisce dì cartone collegate con un ferma-campioni e immaginiamo che esse rappresentino due semirette di cui il ferma-campìone è l’origine comune O.

Partiamo dalla prima posizione (fig. 33 a) in cui la semiretta OB è sovrapposta alla semiretta OA; facciamo poi ruotare la semiretta OB intorno ad OA, nel verso delle lancette dell’orologio, e fermiamola nella seconda posizione (fig. 33 b).

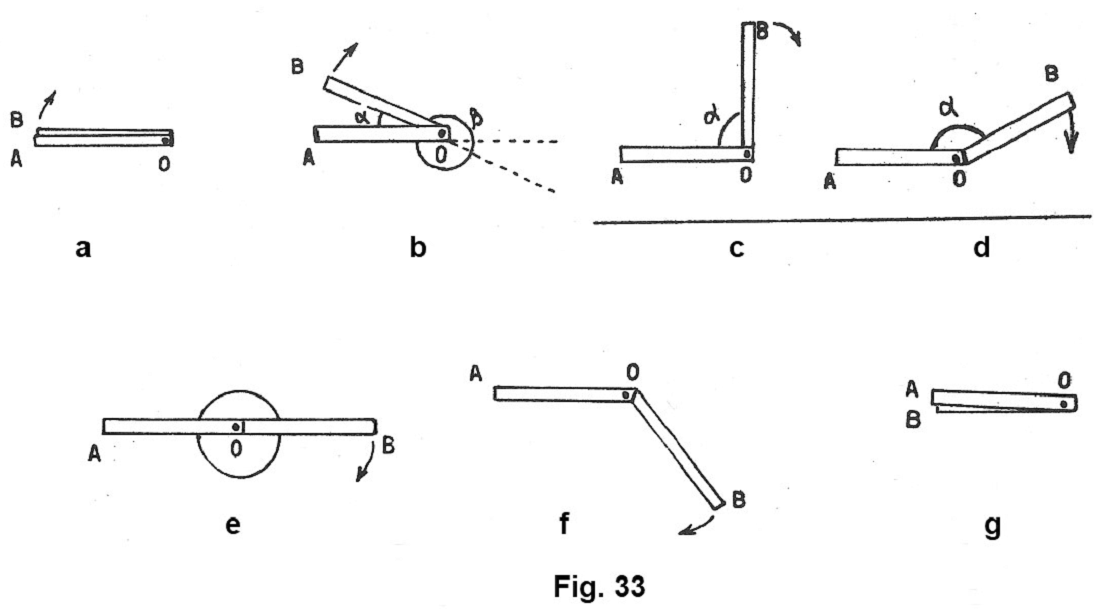
Consideriamo la parte di piano racchiusa tra le due semirette OA e OB (quella contrassegnata dalla lettera α). Il disegno, limitato naturalmente dalla larghezza del foglio, ci rappresenta solo una parte di questa porzione di piano che noi dobbiamo pensare illimitatamente estesa, in quanto le semirette OA e OB sono illimitate. A questa parte di piano racchiusa dalle due semirette OA e OB si dà il nome di angolo di cui OA e OB si dicono lati ed O vertice e si indica con la scrittura: che si legge angolo AÔB (il segno /\ sovrapposto alla lettera O sta ad indicare che O è il vertice dell’angolo).
Quando le semirette OA e OB si trovano nella prima posizione (fig. 33 a), l’angolo si dice nullo.

Osserviamo ancora le semirette che si trovano nella seconda posizione (fig. 33 b). Anche la porzione di piano contrassegnata con la lettera β è un angolo di cui OA e OB sono ancora i lati ed O il vertice.

Perciò, in generale si dice che: un angolo è la porzione di piano compresa tra due semirette aventi la stessa origine.
L’origine O si dice vertice dell’angolo, le due semirette ne sono i lati.
Le semirette OA ed OB possono formare due angoli (α e β) fra i quali vi è una differenza sostanziale.
Infatti se prolunghiamo le due semirette dalla parte opposta all’origine, osserviamo che i prolungamenti sono situati internamente all’angolo β (fig. 34). Per poter distinguere i due tipi di angoli, chiameremo angolo concavo quello che contiene i prolungamenti dei suoi lati (nel nostro caso β), convesso quello che non li contiene (nel nostro caso α).

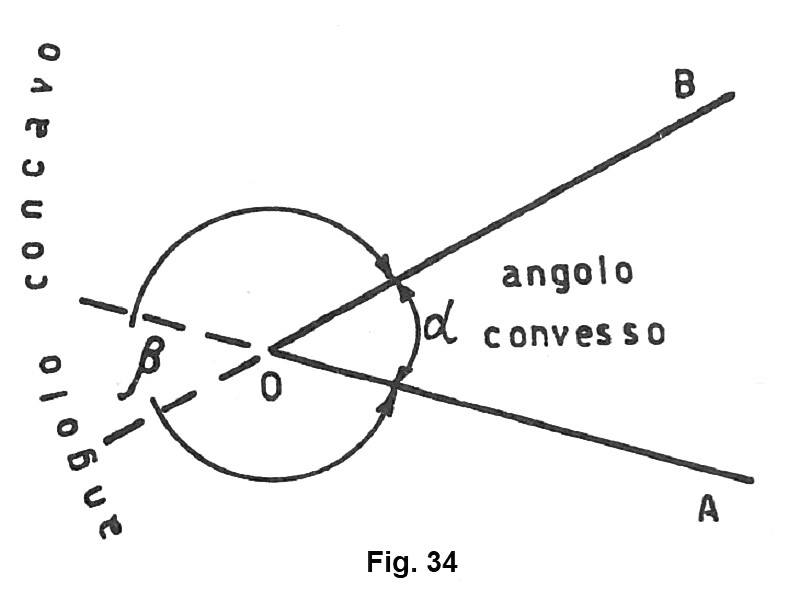
Dato dunque che le due semirette OA e OB della figura 33 b, determinano due angoli, l’angolo AÔB convesso e l’angolo AÔB concavo, dicendo solo angolo AÔB intendiamo parlare solo dell‘angolo convesso (α).

Riprendiamo ancora in esame le due strisce di cartone rappresentate nella figura 33 e continuiamo a far ruotare OB intorno ad OA. Osserviamo la quinta posizione (ﬁg.33 e) e notiamo la posizione che la semiretta OB assumerà, rispetto ad OA: infatti OB verrà a trovarsi sul prolungamento di OA dalla parte opposta di O.

Le semirette divideranno allora il piano in due semipiani. Ciascuno dei due angoli, aventi per lati le due semirette opposte, si dice angolo piatto. Un angolo piatto non è né convesso né concavo.
Continuiamo a far ruotare OB intorno ad OA fino a raggiungere la settima posizione (fig. 33 g), quando cioè le due semirette, dopo la rotazione completa di OB, coincideranno nuovamente. Allora OB avrà descritto tutto il piano e l‘angolo corrispondente si dirà angolo giro.

*** * * * ***

Angoli consecutivi e angoli adiacenti

Disegniamo su un foglio di carta i due angoli qualsiasi AÔB e CÔ’D (ﬁg. 35 a, b) e ritagliamoli. Disponiamoli poi nella posizione indicata dalla figura 35 o, in modo cioè che O’ coincida con O, che i lati O’C e OB coincidano e che O’D e OA siano situati da parte opposta rispetto al lato comune. Due angoli disposti in tal modo si dicono consecutivi.

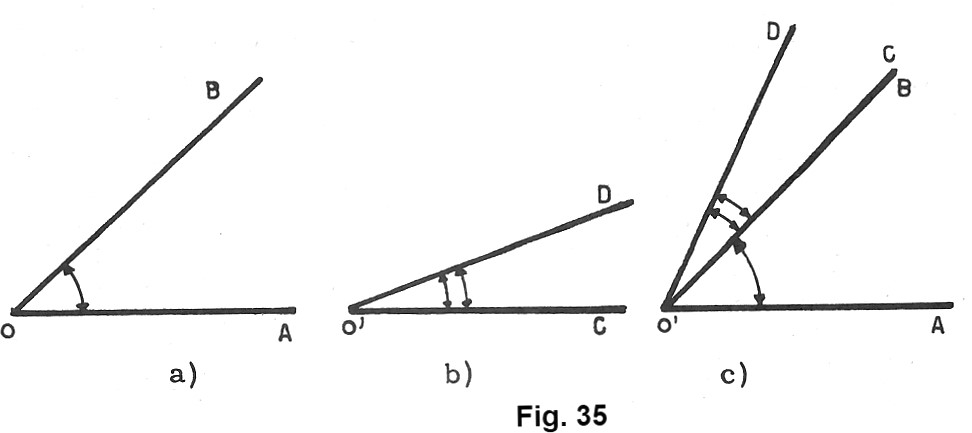
In generale possiamo dire che: due angoli si dicono consecutivi quando hanno il vertice ed un lato in comune e gli altri due lati situati da parti opposte rispetto al lato comune.
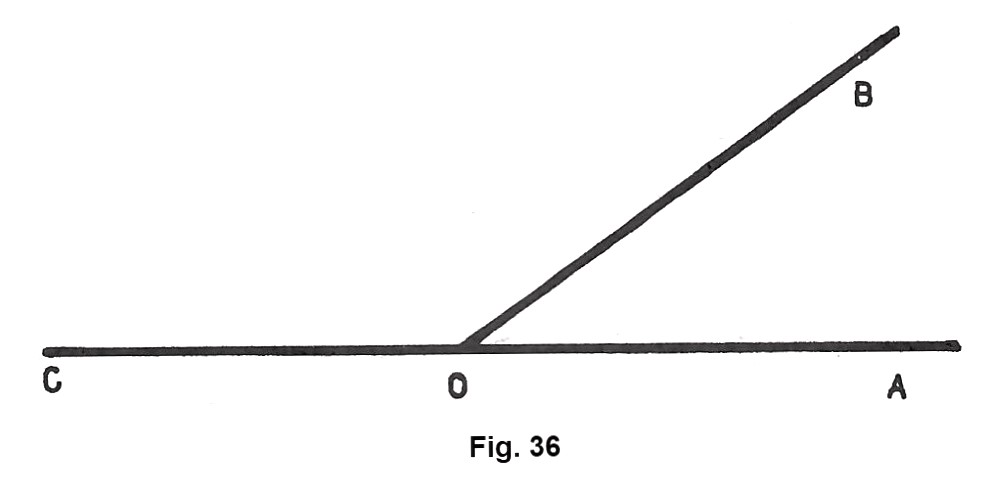
Inoltre che: due angoli consecutivi si dicono adiacenti quando i lati non comuni sono situati l’uno sul prolungamento dell’altro (fig. 36).

*** * * * ***

Confronto di angoli

Tracciamo su un foglio di carta due angoli qualsiasi, ADB e CO’D (fig. 37 a) e ritagliamoli. Trasportiamo l’angolo CÔ’D sull‘angolo AÔB in modo che O’ coincida con O ed il lato O’C con OA. Sì possono verificare tre casi.

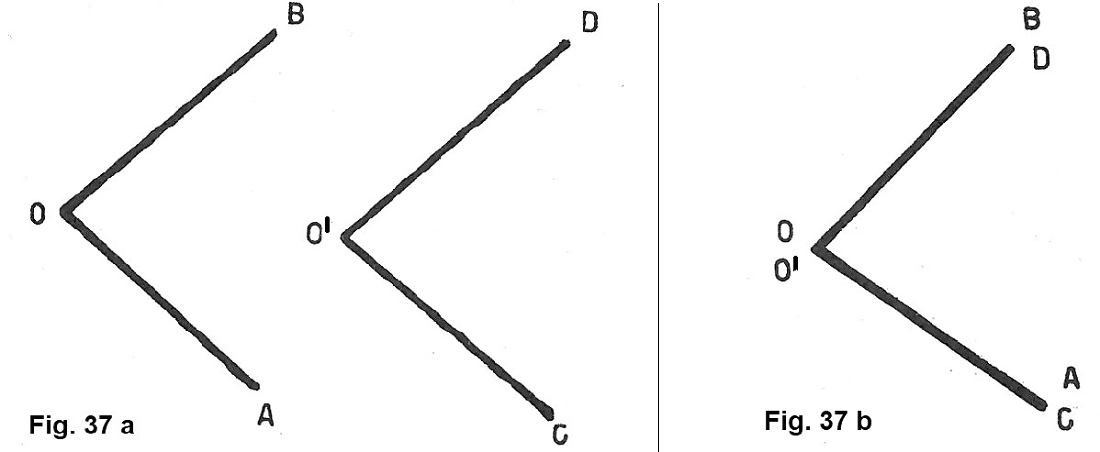
1) Il lato O’D coincide con il lato OB: in tal caso i due angoli sono uguali (fig. 37 b) e possiamo
scrivere: AÔB = CÔ’D.
Quindi: due angoli sono uguali quando è possibile sovrapporli in modo che tutti i loro punti coincidano.

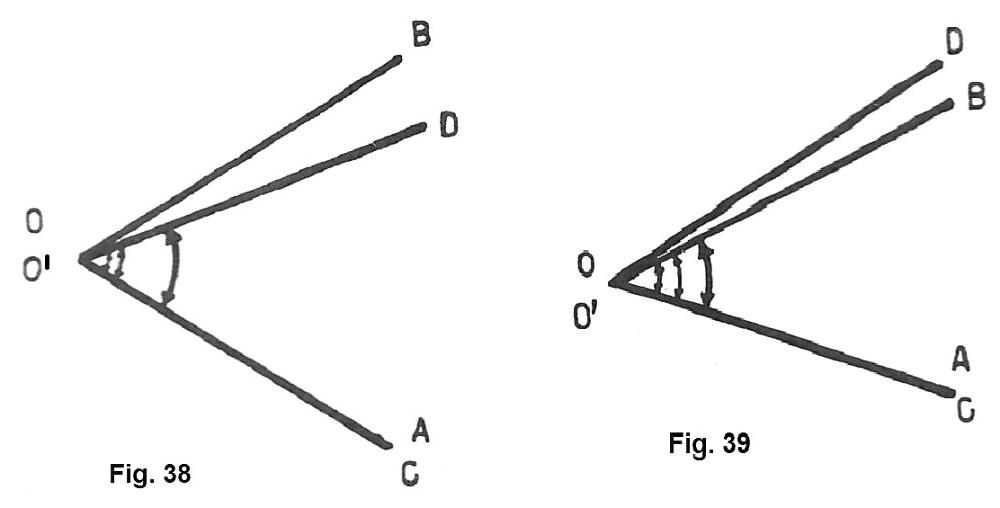
2) Il lato O’D si dispone internamente all’ angolo AÔB: allora i due angoli sono disuguali (fig. 38) e precisamente l’angolo CÔ’D è minore dell’angolo AÔB e potremo scrivere: CÔ’D < AÔB

3) Il lato O’D si dispone esternamente all’angolo AÔB (figura 39): i due angoli sono ancora disuguali e precisamente l’angolo CÔ’D è maggiore dell’angolo AÔB e possiamo scrivere: CÔ’D > AÔB.

*** * * * ***

Angoli opposti al vertice

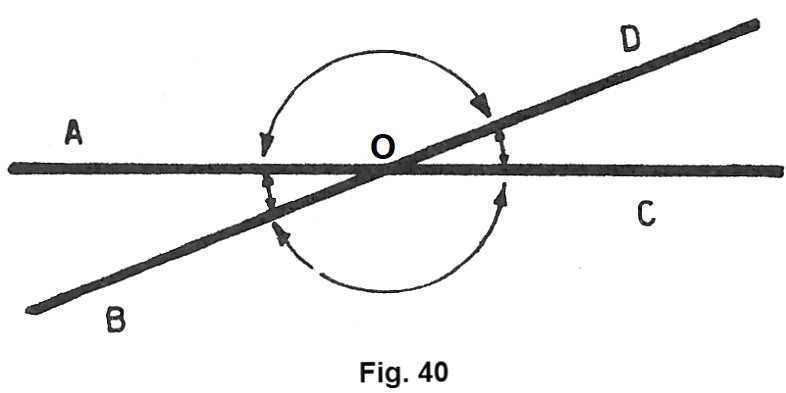
Consideriamo due rette AC e BD incidenti in un punto O (fig. 40). Esse formano quattro angoli e precisamente gli angoli AÔB, BÔC, CÔD, DÔA.

Possiamo facilmente verificare che l’angolo AÔB è uguale all’angolo BÔC.

La verifica sperimentale può essere effettuata ritagliando gli angoli di ogni coppia e sovrapponendoli: essi dovranno
coincidere.

I lati dell’angolo CÔD sono le semirette opposte ai lati dell’angolo AÔB: angoli di questo tipo si dicono opposti al vertice.

Sono opposti al vertice anche gli angoli AÔD e BÔC.

Quindi: due angoli si dicono opposti al vertice se i lati dell’uno sono i prolungamenti dei lati dell’altro. Inoltre: gli angoli opposti al vertice sono uguali.

*** * * * ***

Somma di angoli

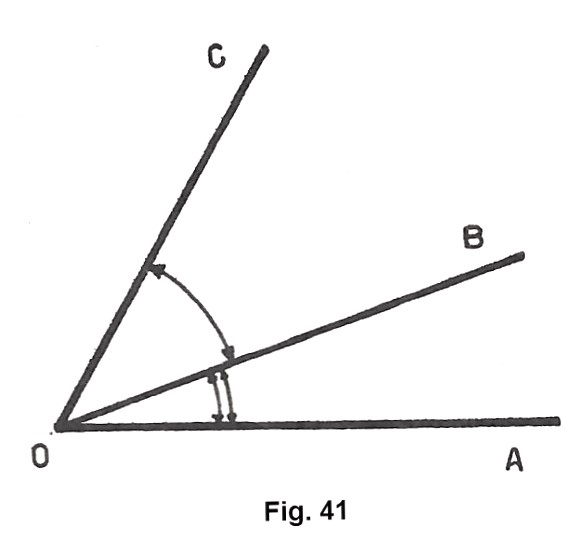
Ritagliamo due angoli qualsiasi AÔB e CÔB e disponiamoli consecutivamente l’ uno all’ altro. L’angolo AÔC, così ottenuto (fig. 41), si dice somma dei due angoli AÔB e CÔB e si scrive:
AÔC = AÔB + CÔB
Perciò diciamo che: per sommare due angoli si dispongono consecutivamente l’uno all’altro; l’angolo ottenuto sopprimendo il lato comune, è la somma.

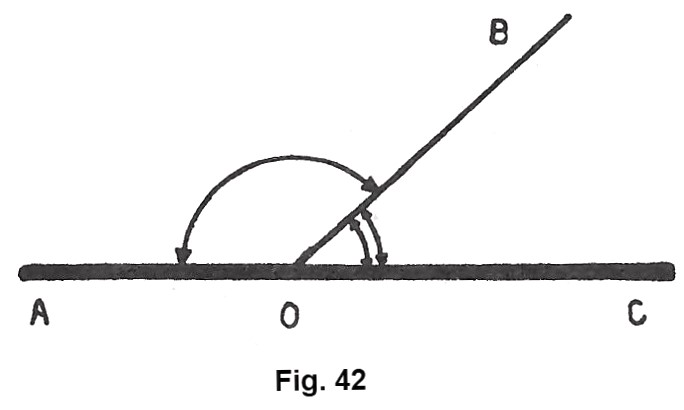
In particolare, quando sommando due angoli si ottiene un angolo piatto (fig. 42), essi si dicono supplementari.
Quindi: due angoli sono supplementari quando la loro somma è uguale ad un angolo piatto,

In particolare: due angoli adiacenti sono supplementari.

*** * * * ***

Differenza di angoli

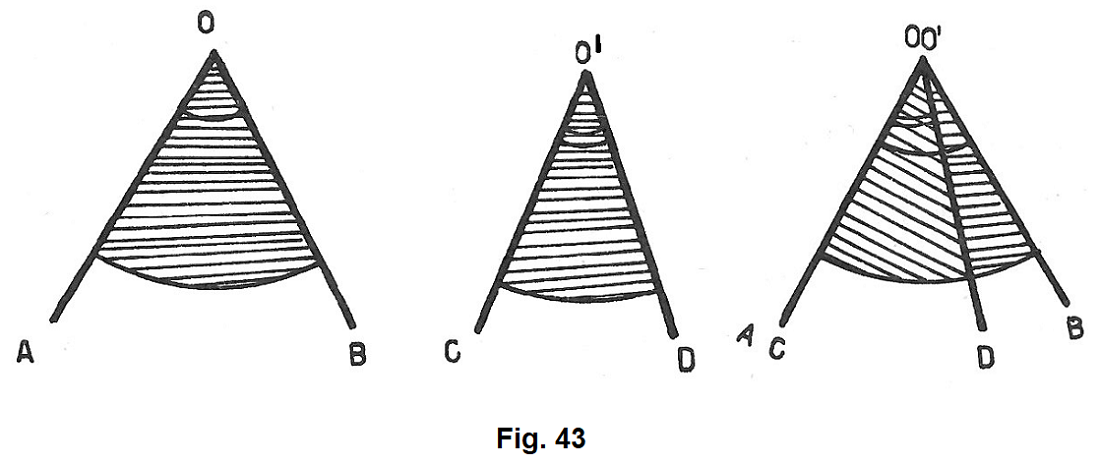
Trasportiamo l’angolo CÔ’D sull’angolo AÔB maggiore di CÔ’D e disponiamoli in modo che O’ coincida con O, O’C con OA e che O’D e OB siano dalla stessa parte rispetto a OA (fig,_43).
L’angolo DOB si dice differenza dei due angoli dati e si scrive: DÔB = AÔB – CÔ’D

*** * * * ***

Multipli e sottomultipli di un angolo

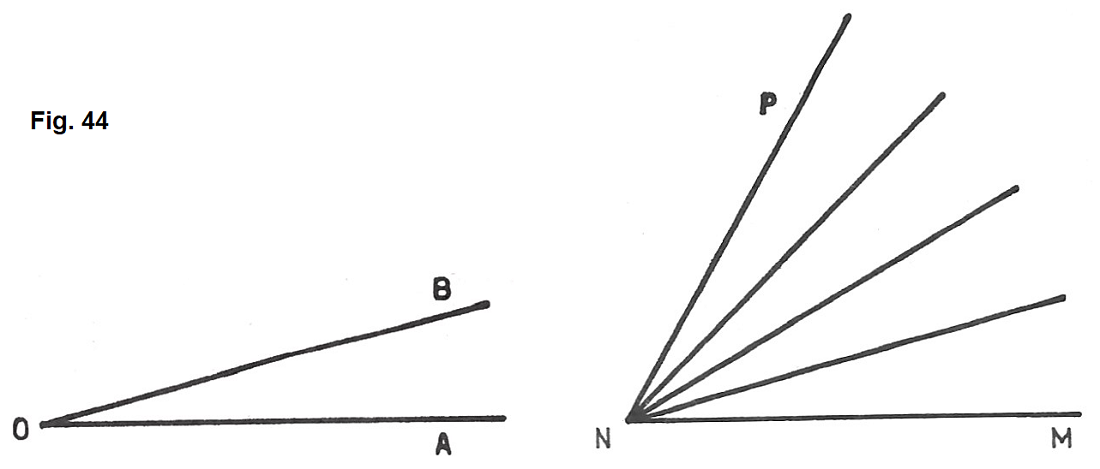
Se disponiamo consecutivamente due o più angoli uguali (fig. 44) otteniamo un angolo somma di due o più angoli uguali. Tale angolo sarà il doppio, il triplo, ecc. di ciascun angolo.

Quindi: un angolo è multiplo di un angolo dato secondo 2, 3, ecc. Quando è la somma di due, tre, ecc. angoli uguali al dato.

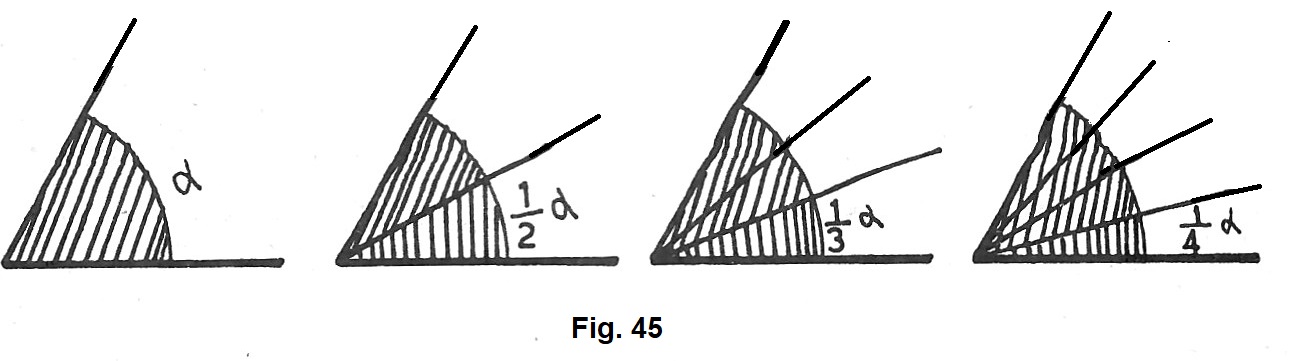
Se invece si divide un angolo in due, tre, ecc. parti uguali (fig, 45 ), ciascuna di queste parti è detta la metà, la terza parte, ecc. dell’angolo considerato, eppure sottomultipla dell’angolo stesso secondo i numeri 2, 3, ecc.

*** * * * ***

Bisettrice di un angolo

Disegniamo l’angolo AÔB su un foglio di carta e ripieghiamo poi la carta in modo che i lati OA e OB si sovrappongano. L’angolo AÔB risulta cosi diviso dalla piega in due angoli consecutivi uguali (fig. 46).
La semiretta OC, che divide l’angolo in due parti uguali è detta bisettrice dell’angolo stesso.

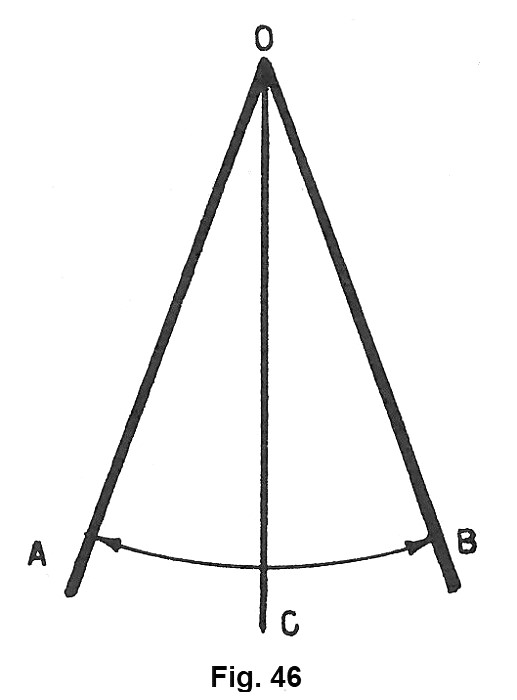
Quindi possiamo dire che: bisettrice di un angolo è la semiretta avente l’origine nel vertice dell’angolo e che divide questo in due parti uguali.
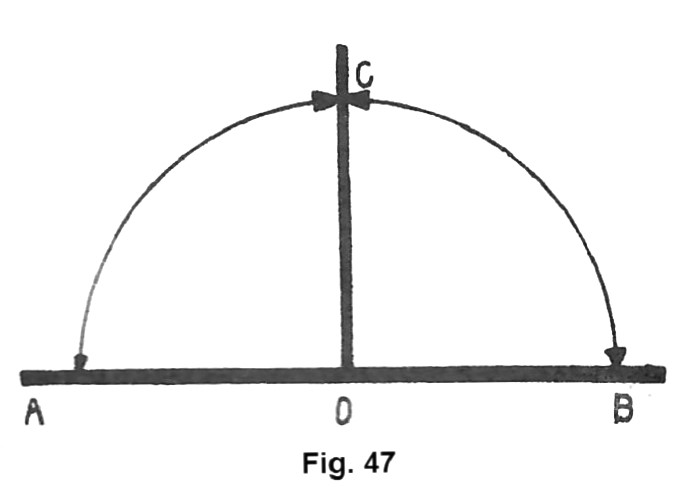
Se costruiamo col metodo precedentemente illustrato la bisettrice di un angolo piatto (fig. 47) otterremo due angoli uguali che prendono il nome di angoli retti. Perciò: un angolo retto è la metà di un angolo piatto. Poiché tutti gli angoli piatti sono uguali, anche tutti gli angoli retti sono uguali.

È evidente che un angolo giro è la somma di quattro angoli retti.

*** * * * ***

Angoli acuti, ottusi, complementari

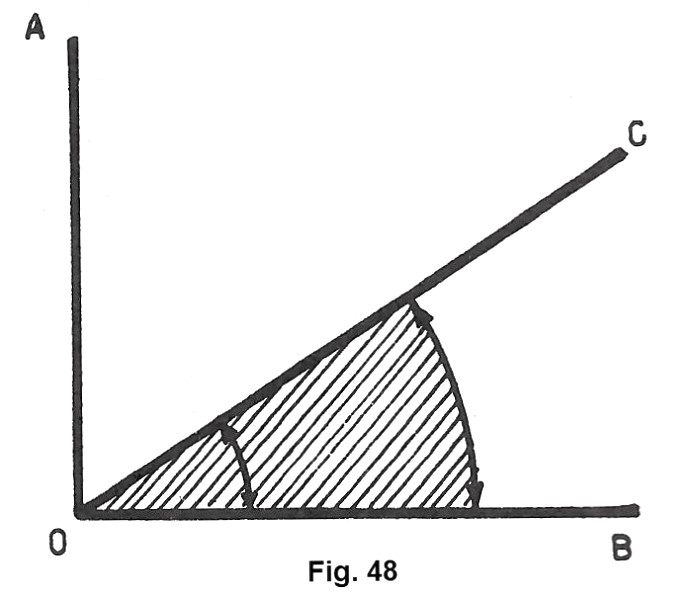
Consideriamo l’angolo retto AÔB e nel suo interno tracciamo la semiretta OC (fig. 48). L’angolo BÔC, cosi formato, è, ovviamente, minore dell’angolo retto e si dice angolo acuto. Quindi: un angolo si dice acuto se è minore di un angolo retto.

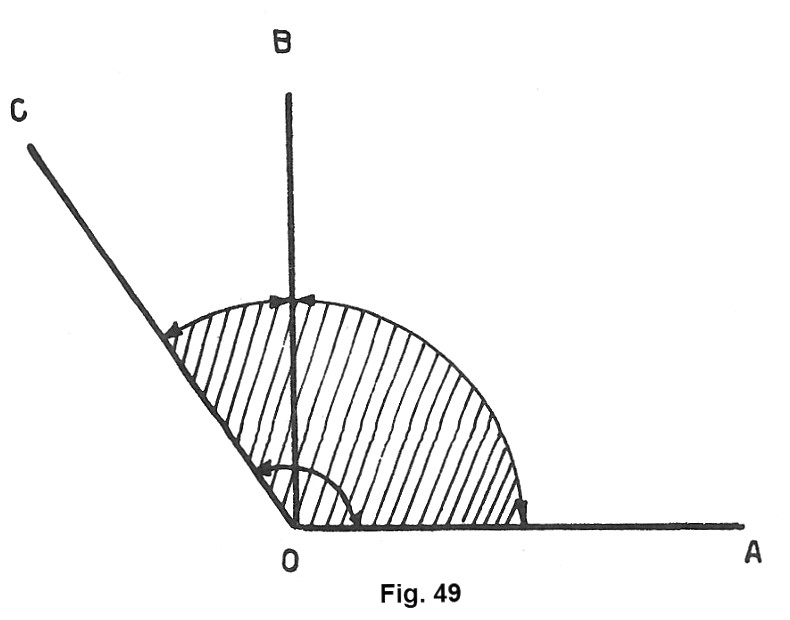
Consideriamo ancora l’angolo retto AÔB e, all’esterno di esso, tracciamo la semiretta OC (fig. 49). L’angolo AÔC, così formato, è maggiore dell’angolo retto, ma minore di un angolo piatto. Tale
angolo si dice ottuso. Perciò: un angolo ottuso è un angolo maggiore di un angolo retto ma minore di un angolo piatto.

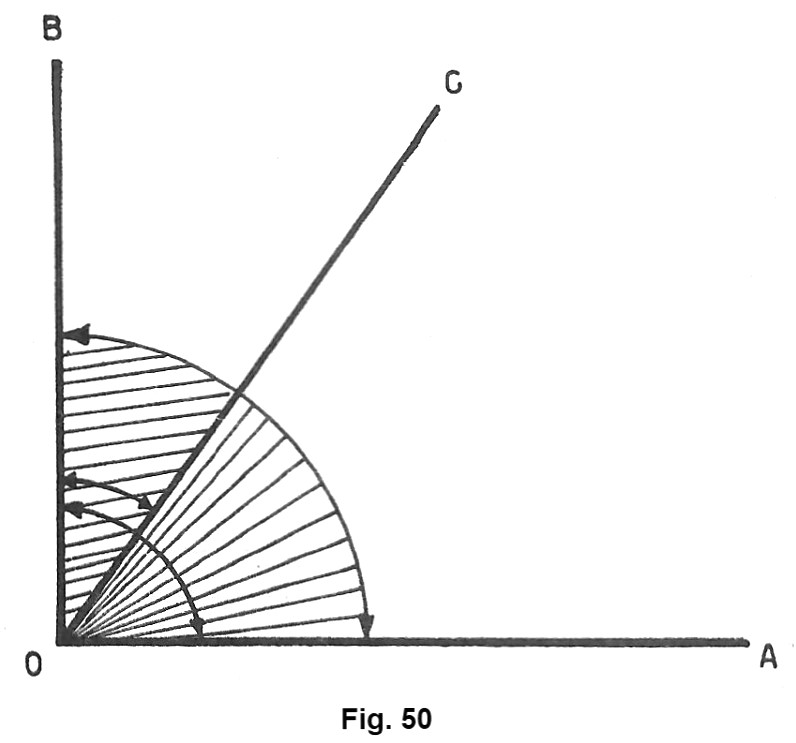
Consideriamo nuovamente l’angolo retto AÔB e tracciamo nel suo interno la semiretta OC che lo divide nei due angoli acuti AÔC e CÔB (fig. 50). Tali angoli hanno per somma un angolo retto: essi sono detti angoli complementari. Quindi: si dicono angoli complementari due angoli la cui somma è un angolo retto.

*** * * * ***

Misura degli angoli

Come per i segmenti, anche per misurare gli angoli bisogna scegliere una unità di misura. A tal fine si assume un angolo come unità di misura e si confrontano poi con esso tutti gli angoli che devono essere misurati.

Misurare un angolo significa confrontarlo con un altro, preso come unità di misura e vedere quante volte l’unità di misura è contenuta nell’angolo considerato. Il numero che si ottiene è la misura o ampiezza dell’angolo rispetto all’unità di misura,

L’ìmità di misura fondamentale per la misura degli angoli è il grado, che è la novantesima parte dell’angolo retto.

I suoi multipli e sottomultipli sono:

multipli
– angolo retto = 90 gradi (90° )
– angolo piatto = 180 gradi (180° )
– angolo giro = 360 gradi (360°)

sottomultipli
– (minuto) primo = 1/60 di grado
– (minuto) secondo = 1/60 di primo

Come già sappiamo dall’aritmetica, queste unità di misura non appartengono al sistema metrico decimale e sono perciò dette misure non decimali. I numeri che esprimono tali misure sono detti numeri non decimali. Ad esempio, per indicare che un angolo è ampio 12 gradi, 15 primi e 20 secondi si scrive il numero non decimale: 12° 15′ 20″.
Per eseguire le operazioni sui numeri non decimali vi sono delle regole pratiche che si trovano in aritmetica.

*** * * * ***

Il rapportatore – goniometro

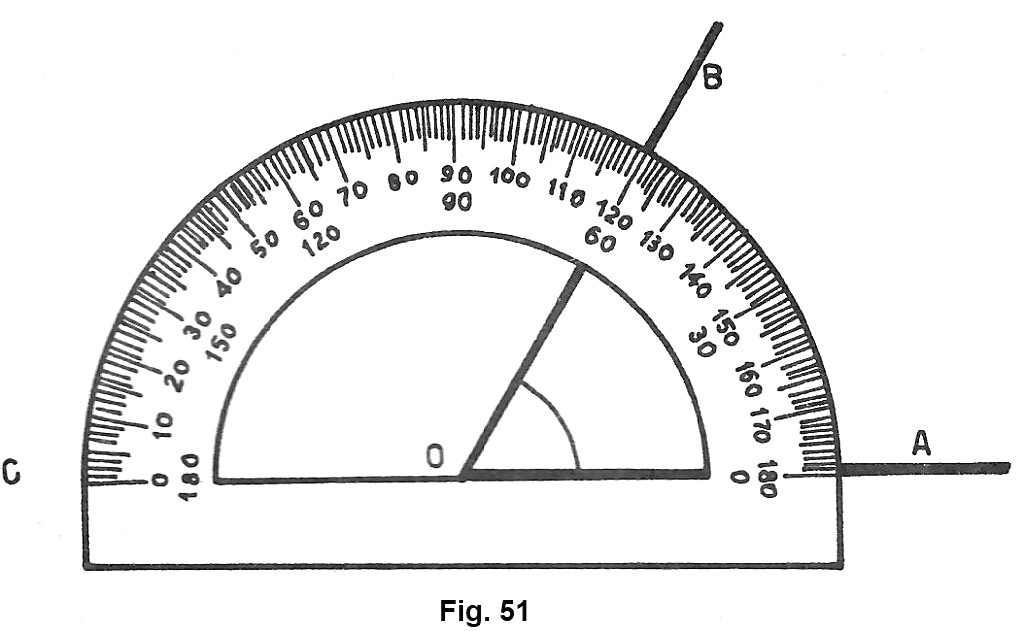
Il più semplice strumento per la misura degli angoli è il rapportatore (fig. 51) o goniometro. Esso è un semi disco di materia plastica o di metallo il cui orlo curvilineo è diviso in 180 parti uguali per mezzo di sottili linee che prolungate concorrono in O. Tali parti corrispondono alla divisione in 180° dell’angolo piatto AÔC i cui lati sono rappresentati dall’orlo rettilineo interno del rapportatore. Per misurare un angolo convesso AÔB si procede nel seguente modo: si appoggia il rapportatore sull’angolo in modo che il punto O coincida con il vertice O dell‘angolo da misurare e che il diametro AC si sovrapponga ad uno dei lati (ad esempio AO). In tal modo lo zero della graduazione si troverà su questo lato. Quindi si legge la misura dell’angolo osservando per quale graduazione passa il lato OB. Se, ad esempio, OB passa per la 60esima divisione del rapportatore, l’angolo AÔB ha l’ampiezza di 60° (sessanta gradi).