RETTE PERPENDICOLARI

RETTE PARALLELE

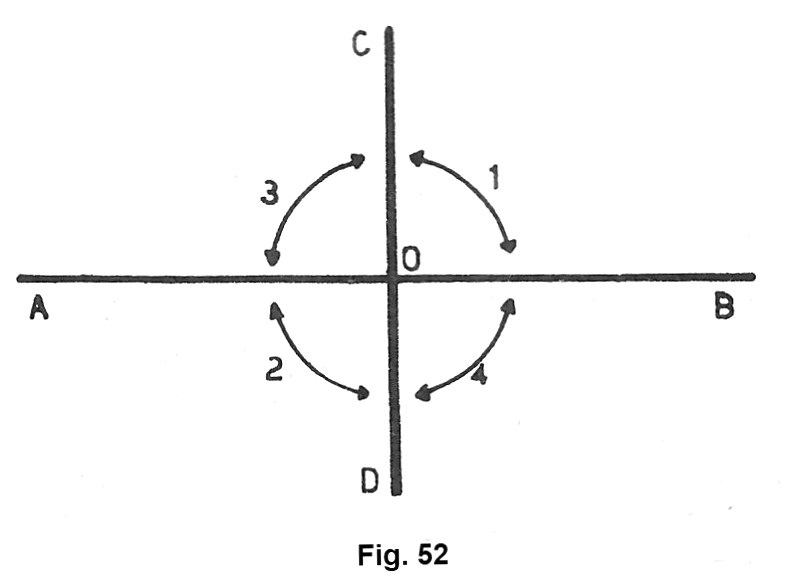
Già sappiamo che quando due rette hanno un punto in comune si dicono incidenti. Quando due rette incidenti dividono il piano in quattro angoli uguali e perciò retti, esse si dicono perpendicolari o ortogonali (fig. 52). Per affermare che due rette sono perpendicolari, basta verificare che è retto uno dei quattro angoli che esse determinano. Infatti se l’angolo (1) è retto, sarà retto pure il suo opposto al vertice (2)e lo saranno anche gli angoli (3) e (4), perché sono entrambi supplementari dell’angolo retto (1).

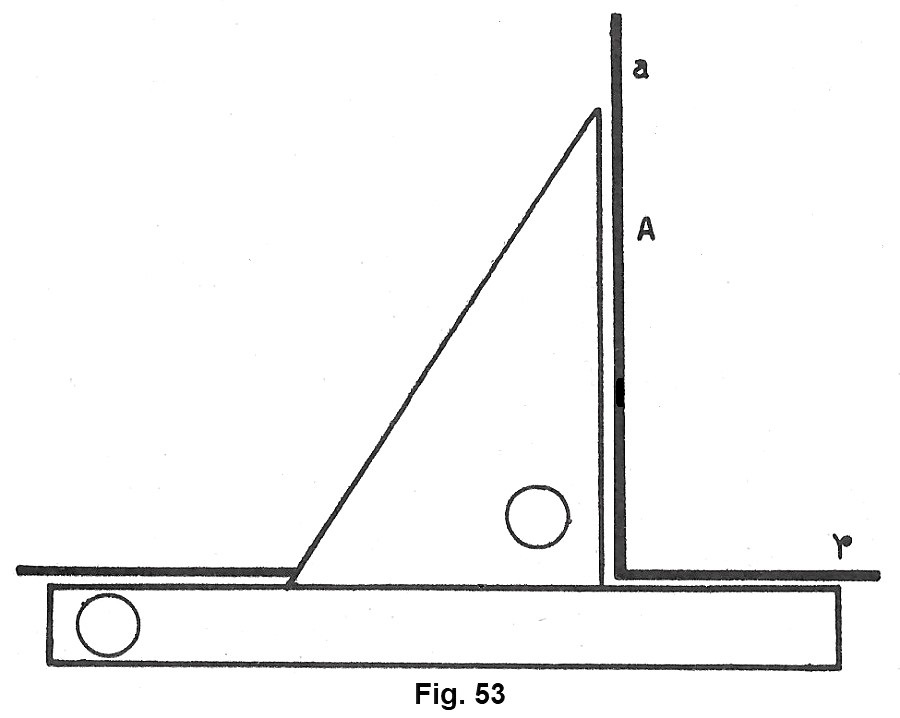
Per tracciare due rette perpendicolari si fa uso della squadra, mediante la quale possiamo condurre la perpendicolare ad una retta r (fig. 53). Basterà disporre una riga in modo che uno dei suoi orli combatti con la retta r. Si fa scorrere uno dei lati minori della squadra lungo l’orlo della riga; facendo scorrere la matita lungo altro lato minore della squadra, si ottiene la perpendicolare richiesta.

*** * * * ***

Distanza di un punto da una retta

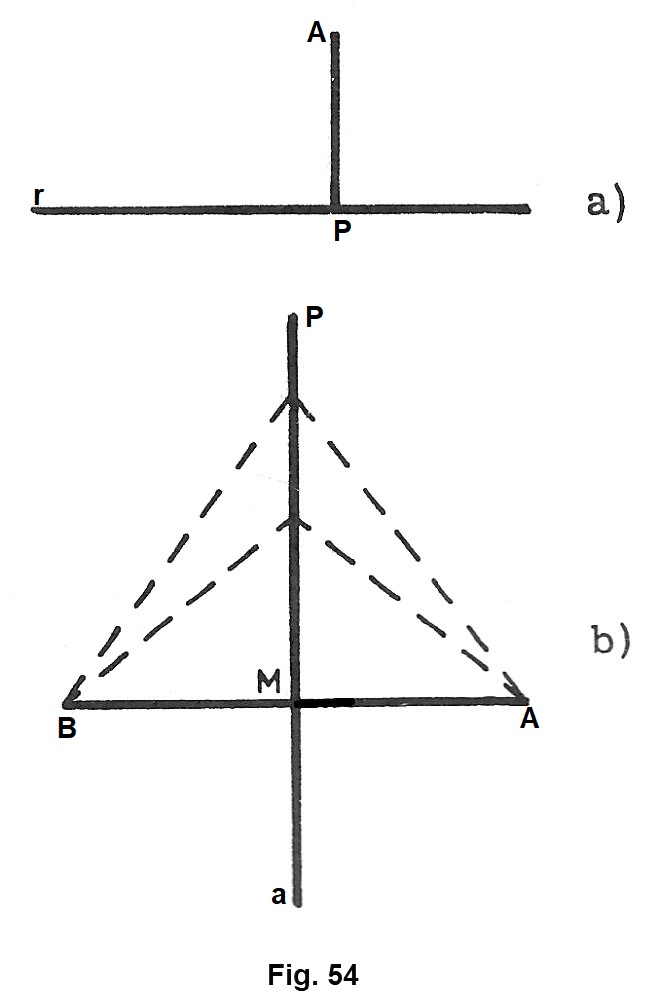
La distanza di un punto A da una retta r è il segmento di perpendicolare condotto dal punto alla retta (fig. 54 a). Il punto P, comune alle due rette, si dice piede della perpendicolare. Il segmento PA, si dice segmento perpendicolare condotto dal punto A alla retta r ed è minore di tutti i segmenti obliqui che uniscono A coi vari punti della retta-stessa, come è possibile constatare dalla figura 54 b.

È importante osservare che, dalle costruzioni precedenti, si può verificare che: dati una retta ed un punto fuori di essa (o posto su di essa), per quel punto passa una sola perpendicolare alla retta data.

Se invece non fissiamo il punto, possiamo ovviamente tracciare infinite perpendicolari alla retta data.

*** * * * ***

Asse di un segmento

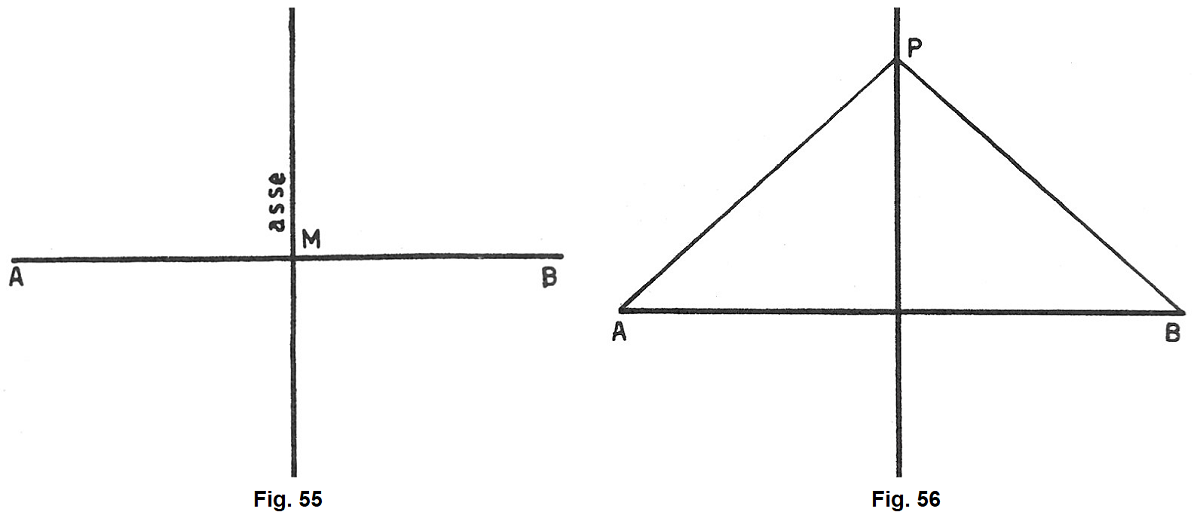
Consideriamo un segmento AB e conduciamo la perpendicolare per il suo punto medio M (fig. 55). Essa prende il nome di asse del segmento. È facile constatare (fig. 56) che ogni punto P dell’asse è situato ad uguale distanza dagli estremi del segmento.

*** * * * ***

Rette parallele

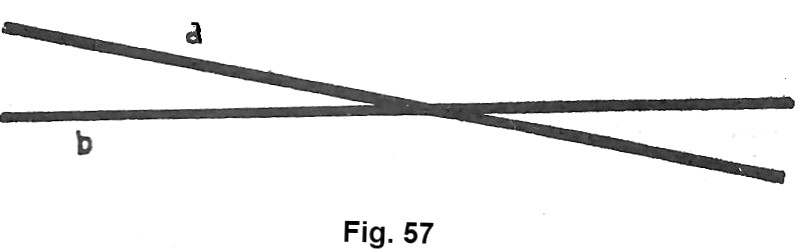
Se disegniamo su un piano due rette a e b è chiaro che abbiamo due sole possibilità di scelta circa il nostro disegno. O le due rette si intersecano o non si intersecano. Se le due rette si intersecano, come già sappiamo, esse si dicono incidenti (fig, 57).

Se non si intersecano si dicono rette parallele (fig. 58). Cioè si può dire che: due rette appartenenti ad uno stesso piano si dicono parallele se non hanno alcun punto in comune. Si intuisce facilmente che due rette parallele conservano sempre la stessa distanza.

Per disegnare due rette parallele, basta disegnare, facendo uso della riga e della squadra, due rette CP e AB perpendicolari a una stessa retta r (fig. 59).

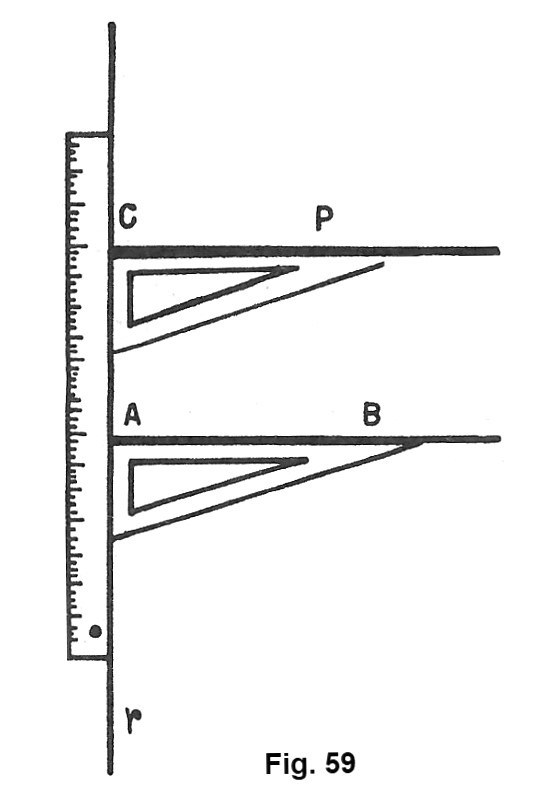
Tali rette non possono avere alcun punto in comune, perché, se lo avessero, passerebbero per esso due rette perpendicolari alla retta r. Ma sappiamo che ciò non è possibile. Perciò: due rette perpendicolari ad una stessa retta sono parallele.

*** * * * ***

Distanza fra due rette parallele

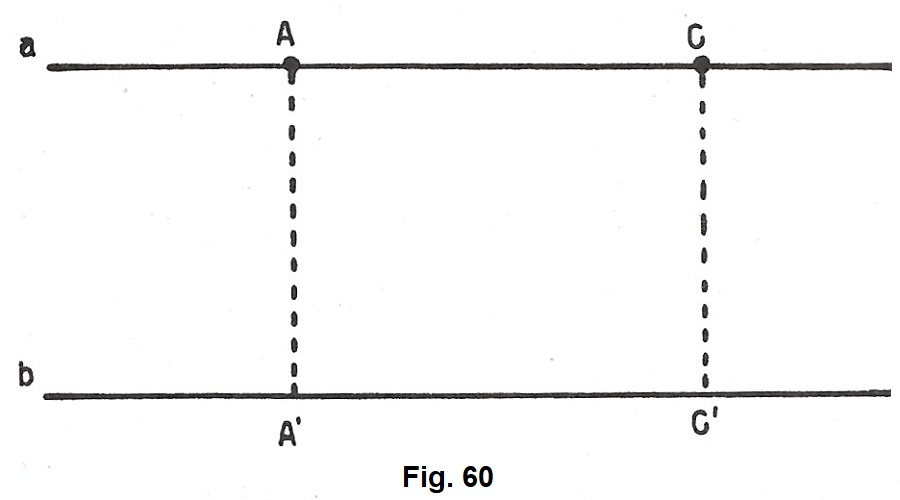
Consideriamo due rette parallele a e b. Prendiamo dei punti qualunque della retta a, ad esempio A e C, e conduciamo per essi le perpendicolari alla retta b. Indichiamo con A’ e C’ i piedi di queste perpendicolari.

È facile verificare che AA’ = CC’ (fig. 60).

Perciò diciamo che: se due rette sono parallele, i punti dell’una hanno uguale distanza dall’altra. Tale distanza si dice distanza delle due rette parallele.

*** * * * ***

Parallela per un punto ad una retta (postulato di Euclide)

Data una retta r ed un punto P fuori di essa, e possibile costruire la parallela alla retta r, passante per il punto P. A tale scapo basterà disporre la squadra sul foglio facendo coincidere uno dei suoi lati minori, ad esempio AB, con la retta r (fig. 61). Si pone poi a contatto con l’altro lato minore CB, l’orlo di una riga e si fa strisciare la squadra lungo la riga finché il lato AB della squadra, che prima coincideva con r, passi per P.

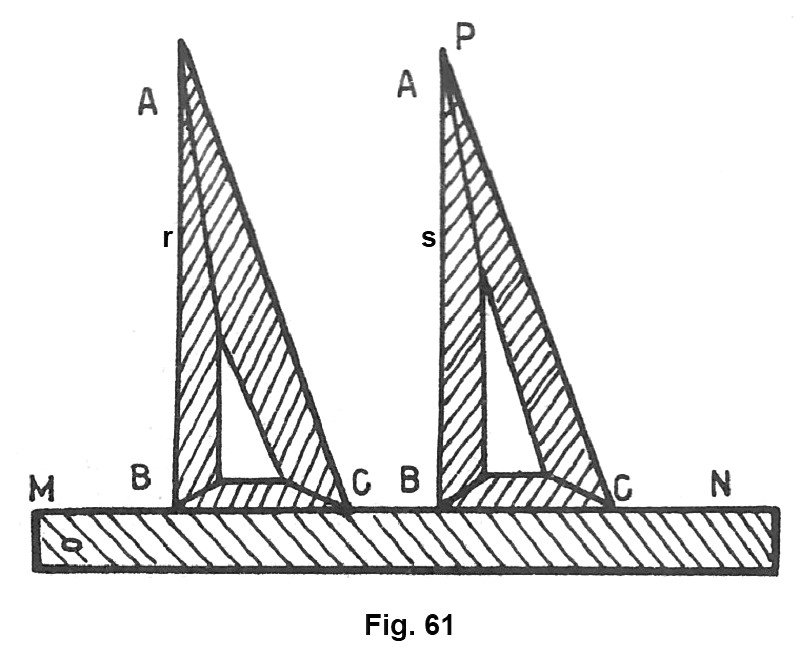
Si fa poi scorrere la matita lungo il lato della squadra e si ottiene la retta s – parallela ad r. Possiamo asserire che le due rette r ed s, sono parallele per costruzione perché sono entrambe perpendicolari all‘orlo MN della riga.

Da questa costruzione si vede che: per un punto esterno ad una retta è possibile condurre una sola parallela ad essa.

*** * * * ***

Angoli formati da due rette tagliate da una trasversale

Disegniamo su un piano due rette qualsiasi a e b ed una retta r, che chiameremo trasversale, che incida le prime
due nei punti A e B.

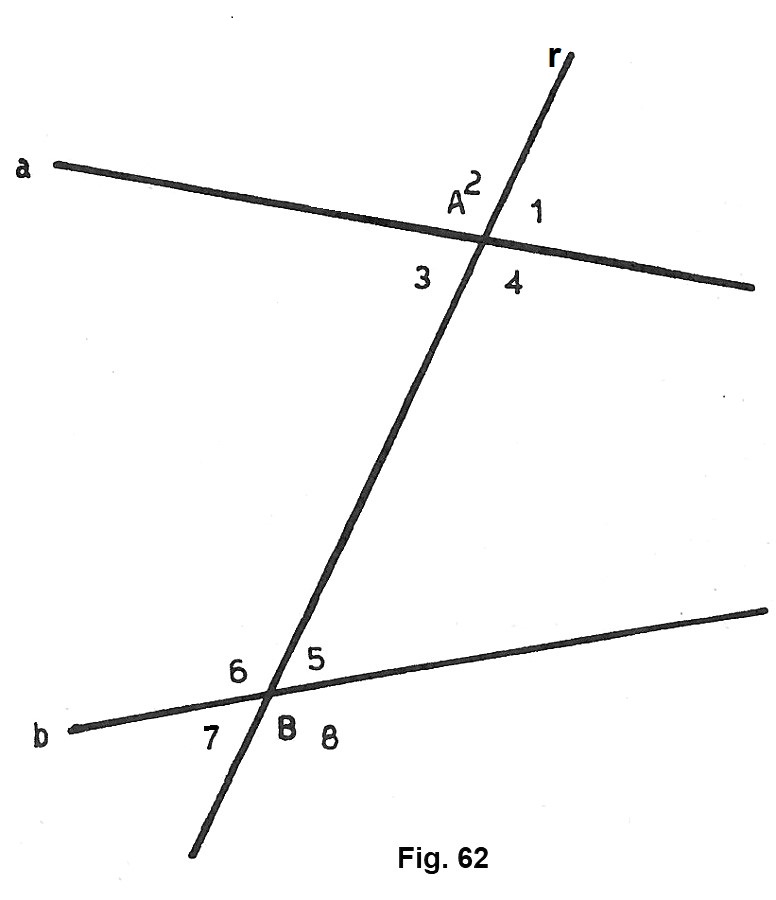
La trasversale r forma con le due rette a e b otto angoli. Si danno particolari nomi ad alcuni di questi angoli, considerati opportunamente a coppie (fig. 62), e precisamente:
1) le coppie di angoli 3-5 e 4-6 si dicono alterni interni;
2) le coppie di angoli 1-7 e 2-8 si dicono alterni esterni;
3) le coppie di angoli 2-6 e 3-7; 1-5 e 4-8 si dicono corrispondenti;
4) le coppie di angoli 3-6 e 4-5 si dicono coniugati interni;
5) le coppie di angoli 2-7 ed 1-8 si dicono coniugati esterni.
Se le due rette a e b sono parallele, gli otto angoli sono legati, come vedremo, da relazioni particolari.

*** * * * ***

Angoli formati da due rette parallele tagliate da una trasversale

Disegniamo su un piano due rette a e b, parallele fra loro, tagliate dalla trasversale r (fig. 63). Mediante il rapportatore, possiamo verificare che:
1) gli angoli alterni (interni od esterni) e gli angoli corrispondenti sono uguali(3-5, 4-6, 1-7, 2-8);
2) gli angoli coniugati (alterni od esterni) sono supplementari (2-6, 3-7; 1-5, 4-8);
3) gli angoli corrispondenti sono uguali (3-6, 4-5, 2-7, 1-8).

Tali proprietà si verificano solo nel caso che le rette siano parallele. Perciò possiamo stabilire il seguente criterio di parallelismo: due rette sono parallele se, tagliate da una trasversale, formano:

a) angoli alterni uguali, oppure

b) angoli corrispondenti uguali, oppure

c) angoli coniugati supplementari.